かけ算の順序の昔話

算数教育について気楽に書いていきます。

「盗難事件に関する問題」の整理

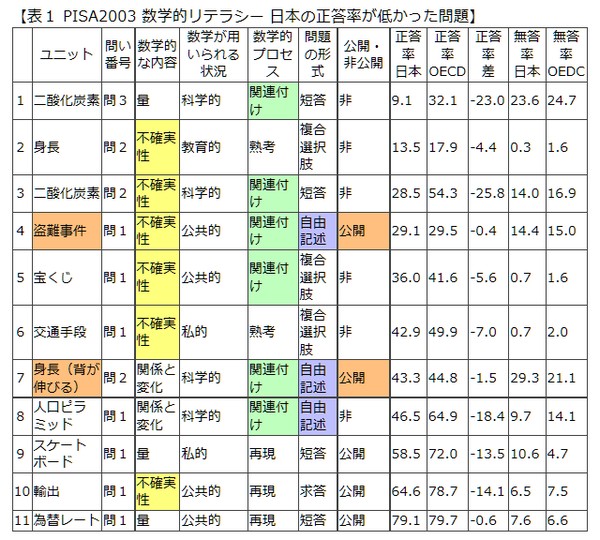
　「盗難事件に関する問題」は，批判的な考察が行えるかどうかの例題として，よく参照されます。これは，PISA2003の数学的リテラシーの調査問題のうち，日本の正答率が，公開された中で最も低かったものです。正答率の算出には，完全正答率＋部分正答率×0.5という，全国学力テストを含め国内の学力調査では見られない方法が採用されています。


　本記事作成のきっかけは，今月発売の雑誌に連続して掲載されている，以下の解説記事を目にしたことです。

  • [清水2017] 清水美憲: 事象を多面的に捉えて批判的に考えるための算数のメガネ, 算数授業研究, Vol.112, pp.12-15, 東洋館出版社 (2017).
  • [青山2017] 青山和裕: 統計的な問題解決と批判的な考察, 算数授業研究, Vol.112, pp.16-19, 東洋館出版社 (2017).

算数授業研究 Vol. 112 論究 XI

算数授業研究 Vol. 112 論究 XI

　雑誌には「論究XI」というナンバーが振られ，「「統計」を究める」と題して特集が組まれています。上記2つの記事で別々に，PISA調査の「盗難事件に関する問題」を取り上げています。
　この問題は，http://www.mext.go.jp/a_menu/shotou/gakuryoku-chousa/sonota/071205/002.pdf#page=23より読めます*1。

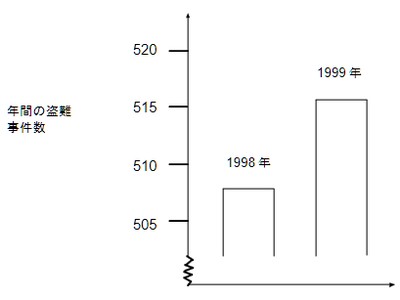
　あるTVレポーターがこのグラフを示して、「1999年は1998年に比べて、盗難事件が激増しています」と言いました。
f:id:takehikoMultiply:20170831230526j:plain
　このレポーターの発言は、このグラフの説明として適切ですか。適切である、または適切でない理由を説明してください。

　この問題に対し，[清水2017]では以下のように解説しています(p.15)．盗難事件数のグラフを含め，問題文そのものは，掲載されていません。

　過去に話題になった代表例には，OECDによるPISA2003年調査の「盗難事件」の問題がある(略)。これは，一部が省略されたグラフから，盗難事件の発生数の増加の傾向を把握する問題であった。日本の生徒の平均正答率は29.1%で，OECD加盟国平均の29.5%よりも低かった。データを注意深く読み取って，その妥当性について批判的に考察するには中学校修了時でも課題があるのだ。

　この段落だけを読むと，正答率の「日本…29.1%」「OECD加盟国平均…29.5%」は，「低かった」というよりも，「ほぼ同じ」と思わずにはいられません。またトップの国は何%だったのかなど，国ごとの状況なども書かれていません。
　Googleで検索してみたところ，同じ著者による2007年の文章がヒットしました。

（１）表やグラフから適切に情報をよみとること
　PISA2003年調査の「盗難事件」（Figure1）は，一部が省略されたグラフから，盗難事件の発生数の増加の傾向を把握する問題であった。日本の生徒の平均正答率は29.1%で，OECD加盟国平均の29.5%よりも低かった。また，フィンランドの生徒の平均正答率は45.8%であった。
（Figure1：省略）
　同様な問題には，「輸出」（日本の平均正答率64.6%; OECD平均正答率78.7%），PISA2003予備調査問題「二酸化炭素排出量の減少」，PISA2003枠組みの例示問題「犯罪の増加」などがある。
　これらの問題は，与えられた表やグラフから適切に情報を読み取ることを求める問題である。このような力の育成が，日本の数学教育における課題となっている。

　[青山2017]に視点を移しますと，p.19に，盗難事件数のグラフとともに問題文が囲まれています。同じ著者による，「研究動向からみた統計リテラシー」と題する2ページの解説*2でも言及されており，正答率については「この問題での日本の生徒の正答率は，全体で29.1%となっている。オーストラリア，カナダなど40%超の国が3ヶ国，30%超の国は6ヶ国，OECD平均が29.5%と日本の正答率はかなり低いものとなっている。」と記されています。
　「盗難事件に関する問題」が注目されている理由として，PISA2003の数学的リテラシーの調査問題のうち，公開された中で最も低かったというのがあります。以下のページで，表を見ることができます。

f:id:takehikoMultiply:20170831230546j:plain

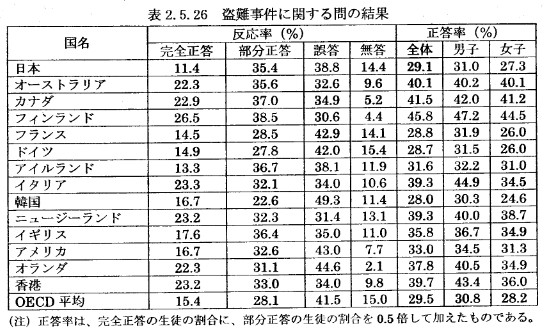
　国ごとの違いのほか，解答類型や採点方法は，http://www.ocec.ne.jp/linksyu/pisatimss/sugakuriterasi.pdfより知ることができます。「盗難事件に関する問題」はp.19からです。完全正答（2点），部分正答（1点），誤答／無答（0点）の類型が書かれたのち，国ごとの表が掲載されています(p.22)。

f:id:takehikoMultiply:20170831230559j:plain

　「正答率は，完全正答の生徒の割合に，部分正答の生徒の割合を0.5倍して加えたものである。」という注も，興味深いところです。全国学力テストなど，国内の学力調査で，この方式で正答率を算出するものは見かけません。
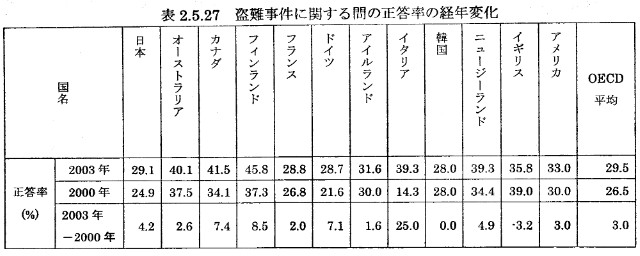
　また次のページには，2000年と2003年との各国およびOECD平均の，正答率の変化が表になっています。

f:id:takehikoMultiply:20170831230615j:plain

　まず表2.5.26を見て驚くのは，日本が「完全正答」の反応率は，表に記載の中で最も低いのに，全体の正答率となると，OECD平均よりも少し低いくらいになっていることです。これは，先ほど「0.5倍して加えた」と書いた，部分正答の反応率の高さによると言えます。完全正答の割合が高ければその分，部分正答の割合は低くなるため，部分正答の反応率に関して順位をつけるのは不適切ですが，日本は35.4%で，OECD平均の28.1%よりも高く，正答率の高い各国と同程度にあると，見ることができます。
　経年変化の表2.5.27の中で，目につくのは，最下段のイタリアの「25.0」という，正答率の向上のところです。これこそ「激増」です。2000年で，記載された中では最下位のイタリアが，2003年にはトップクラスにまで上がっています。
　ですがこの2回のPISA調査の間に，イタリアが教育面においてめざましく向上したというわけでもなさそうです。
　それよりも「盗難事件に関する問題」については，採点基準に依存するところがあります。具体的には，誤答／無答のコード01と，部分正答のコード11，完全正答のコード21，23について，境界があいまいであり，採点者泣かせの答案が出てきそうに思えます。とくにコード21および23によると，グラフからの数の読み取りや，増加率の計算といった，数的処理のない解答でも完全正答扱いとなり得えます。2000年は厳しめに採点したが，国ごとの比較がなされるのであれば，2003年には甘く採点しよう，という心がわき上がらないとも限りません。
　とはいえ本記事の意図は，算出された正答率を，無視しようというものではありません。正答率に着目して読んでいくと，「100%に近づける努力」は学校の先生方だけでなく，学力調査の採点の段階においても，生じることを知ったのが，最大の収穫でしょうか。
　この種のグラフに対して，児童・生徒らが批判的に考察できるようになる方法として，類似問題を解かせるのと別に，自分で作ったグラフには，そこから読み取るべき事項を，数値を含めて簡潔な文として添える習慣をつけることを提案します。「盗難事件に関する問題」のグラフであれば，「1年で8件増加した。」がその文例となります。


　上記には入れられませんでしたが，「盗難事件に関する問題」「省略棒グラフ」と関連する情報にリンクします。

　それと，http://www.mext.go.jp/a_menu/shotou/new-cs/1387014.htmよりダウンロードできる『小学校学習指導要領解説算数編』*3によると，棒グラフは第3学年で，折れ線グラフは第4学年で学習しますが，縦軸を一部省略したグラフの実例は，「盗難事件に関する問題」を挙げたp.306以外にはなく，その種のグラフを作ることの指導は見当たりません。

*1:書籍だと，isbn:4324075719を，多くの情報源が挙げています。

*2:http://estat.sci.kagoshima-u.ac.jp/SESJSS/data/edu2004/06_aoyama.pdf

*3:[清水2017]，[青山2017]とも，今年公表の『小学校学習指導要領解説算数編』への言及が見当たりませんが，算数授業研究 Vol.112に掲載の他の記事では参照されています。

かけ算・わり算のフラッシュカード

Guiding Children's Learning of Mathematics With Infotrac

Guiding Children's Learning of Mathematics With Infotrac

　1桁×1桁のかけ算と，わり算について，瞬時に答えられるようにするためのフラッシュカードが紹介されていました(p.324)。
f:id:takehikoMultiply:20170824054155j:plain

　左側の(a)のカードには，赤で「63」，緑で「7」と「9」が書かれています。先生の側は，「63」を隠して子どもたちに見せると，子どもたちは「（7×9＝）63」と答えます。「7」を隠して見せると，答えは「（63÷7＝）9」となり，「9」を隠せば，「（63÷9＝）7」です。
　右側の(b)ですが，1枚の紙の表面(Front)に，外周には0から9までがランダムで並んで赤で書かれ，中心には緑で「×8」とあります。裏面(Back)は，外周には0および8の倍数が青で，中心は「÷8」が緑で書かれています．
　ただし表裏の外周の数は，互いにランダムではなく，規則性があります．表面の赤色の数に，8をかけて得られる積は，裏面では左右で見てちょうど反対の場所に配置されます。
　こうすることで，例えば先生が，表面を子どもたちに向け「6」を指でさして，子どもたちが「（6×8＝）48」と答えたとき，指さしている箇所の裏面の数とが同じになることから，正解なのが確認できるようになっています。間違った数を言ったら，指さす位置をそのままにして，このカードを左か右に180度，回転させれば，子どもたちには正解の数が見えることになります。わり算の問題も同様です。
　一つの数に，外周の数を一つずつかけて答えを言う，というのは，日本でも見かけます。以前に事例整理をしていました。

　今回の(b)のフラッシュカードは，かけ算とわり算を同時に練習する際に有用そうに見えました。「8×」ではなく「×8」となっているのは，米国のかけ算の「8の段」だからと考えられますし，「8をかける」と「8でわる」という操作の対称性と解釈することもできます。

2の倍数は，偶数

　https://twitter.com/flute23432/status/896650436266008576から始まるツイートに触発されて，「倍数」の学習や出題に関する事例調査を試みました。
　調査結果の前に，改めて問題意識を言葉にしておきます。数学において2の倍数と言えば「0，±2，±4，…」です．なのですが，小学校では負の数を扱わないから「0，2，4，…」となるのか，というとそうではなく，0も除外し「2，4，6，…」と書くのがどうやら一般的です。算数と数学のギャップについてどのように理解し，またこれまで指導・評価されてきたのか，するとよいのかを，Webで読める情報を通じて探ろうと考えたのでした。
　小学校での学習やテストにおいて，倍数を考える範囲を明示するというのは，容易に思い浮かぶ対応策です。
　例えば，平成29年度 大妻中野中学校 シンガポール会場入学試験*1では，「1から200までの整数を考えます。」から始まって，3の倍数や5の倍数などの個数を出題しています。こう書いてあれば，0のことを考える必要はないわけです。
　範囲の明示は，米国Common Core State StandardsのMathemaicsにおいて，約数(factor)・倍数(multiple)の学習事項でも，取り入れられています。Grade 4のGain familiarity with factors and multiples.には，"whole number in the range 1-100"が3回，出現します。"whole number"だけであれば，（日本の）小学校算数の「整数」に対応し，0，1，2，3，…のことです。"in the range 1-100"により，その段階での約数・倍数の学習では値が限定されるけれど，後にはその限定を解除して考えることも可能となります。
　なお，whole numberの定義はwhole number＝整数は、正しい？｜特許翻訳 A to Zで整理されています。その中で，"zero or any positive multiple of 1"という定義もありますが，このmultipleは，倍数というよりは，整数倍（positiveとあるので正整数倍）と解釈するのがよさそうです。
　倍数の出題例をWebで検索して，よく目にするのは，倍数や公倍数を，小さな数から順に，指定した個数だけ答えさせるものです*2。その際に0を含めないのが，暗黙の了解事項となっています。
　例えば，学ぶ 教える.COMの倍数と約数では，問題５・問題７が該当します。
　教材出版 学林舎のhttp://gakurin.co.jp/topnewimage/toppdf/tikara/tikarakkauninsei.pdf（現在はデッドリンク）において，「倍数の求め方」「公倍数の求め方」に出現します。倍数・公倍数は「小さいものから順に5つ」なのに対し，約数・公約数は「すべて」です。
　株式会社 認知工学が提供しているhttp://ninchi.sch.jp/sample/s35sample.pdfの例題１には「2の倍数を小さいものから5個書き出してみましょう」とあり，答えは「2」「4」「6」「8」「10」です。そして直後の「2の倍数は、偶数とも言います。」を見て，2の倍数と偶数との違いを，さらっと記してあるように感じました。
　「2の倍数は、偶数とも言います」を「xが2の倍数であれば，xは偶数である」に置き換ることができます。しかし，小学校算数の範囲で「偶数は、2の倍数とも言います」や「xが偶数であれば，xは2の倍数である」は言えないのです。0は偶数だけれど，2の倍数に入れないからです。
　『トップクラス問題集』では小学4年に倍数が出てきます。https://books.google.co.jp/books?id=LXy7iCAV8z8C&pg=PA8には「12と30と50の公倍数で3番目に小さい数を求めなさい。」とあります。公倍数に0を含むか否かで答えが変わりますが，残念ながら解答は参照できません。
　「小さい数から順に」のほか，数直線上で倍数を○で囲むのが教育開発出版株式会社によるhttp://www2.kyo-kai.co.jp/img/material/shou/2990/2015pira_5s_sample.pdf（現在はデッドリンク）に見られます。数直線の「0」が薄くなっています。その一方で，「ただし，0は倍数に入れない。」には網掛けが施されています
　今年出版された本に，気になる出題がありました。『すいすい解ける! 中学数学の文章題 驚異のサザンクロス方式』*3です。Googleブックスで一部を読むことができ，https://books.google.co.jp/books?id=v9NTDgAAQBAJ&pg=PA99 の⑧は「自然数nを用いて、4の倍数を表せ。」となっています。答えは「4n」です。この場合，0や-4などは，4の倍数に入らないことになってしまいます。
　学習指導要領・解説からいくつか取り出します。新しい小学校学習指導要領解説の算数(1)のPDF文書内に，「例えば，「整数」，「比例」という用語は小学校で初めて学習するが，中学校では負の数を学習する際に，これらの用語の意味を捉え直す必要がある。」という文があります。
　算数の「整数」は数学の「整数」と異なり，例えば前者はwhole number，後者はintegerと書き分けられます。
　whole numberをnatural number（1，2，3，…）に置き換えて0を除外するという，解釈あるいは書き方がしばしば見られ，倍数・約数や「整除」においても該当する，というのが，当ブログでの基本的なスタンスとなっています。
　昭和33年の小学校学習指導要領 算数*4では，「約数」「倍数」は第5学年の用語に入っています。指導上の留意事項に「(５)　倍数，約数の指導は，分数の計算に必要な程度にとどめること。」とあり，ここでも0は除外と言っていいでしょう。
　高校の（現行の）学習指導要領解説には，「約数と倍数」の中で，「二つの整数a，b（a＞0）について，b＝aq＋r（r＝0，1，2，…，a－1）という表現や割り算の余りによる分類を利用して整数の性質を考察させることも考えられる。」と記されています。bは0であってもよいので，この段階では0は2の倍数に含まれると読めます。
　先月出た中学校学習指導要領解説数学編には，「連続する三つの整数の和は3の倍数になる」が2回，出現します。意図としては文字式で表し証明することなのですが，「連続する三つの整数」として，-1，0，1を考えてみますと，（-1）＋0＋1＝0となり，和は0です。この段階で，0を3の倍数から除外するのは都合が悪い，0を3（や他の正整数）の倍数に入れよう，と指導をするのはどうでしょうか。

*1:http://www.otsumanakano.ac.jp/admission/pdf/2017_singapore_sansu.pdf

*2:ざっと見た限りでは，0を含むいくつかの整数が並んであり，その中から2の倍数などを選ぶような出題は，見当たりませんでした。

*3:isbn:9784408456263

*4:http://www.nier.go.jp/guideline/s33e/chap2-3.htm

算数教育への批判と『小学校学習指導要領解説算数編』の記載，Ver.2をリリース

f:id:takehikoMultiply:20170810060550p:plain

　6月30日にツイート（http://twitter.com/takehikom/status/880523010129645568）し，当ブログでは学習指導要領解説における「弁別」の使用についてで貼り付けた図について，バージョン2を作成しました。Googleドキュメントにて，https://docs.google.com/spreadsheets/d/1mJ9sq72C2Qp7uKycF0iebRhXTEoOT6bMLHR4lmE104Q/edit?usp=sharingよりスプレッドシートの参照と，Excel形式によるダウンロードができます。
　修正点は以下のとおりです。

  • 「0.2＋0.8＝1.0が間違いなのはおかしい」と「「はした」は理解しにくい」の行を追加しました。
  • 各項目の該当学年が分かるよう列を設けました。
  • 「現行を踏襲し、「長方形の紙を折って正方形を作る」が追加」を「「正方形や長方形を弁別できるようにすること」が追加」に変更しました。
  • ワークシートの「sources」を取り除き，「claim」を「table」に変更しました。


　リンク集です。

　批判の事例については，https://twitter.com/takehikom/status/895392968374329344より始まる一連のツイートをご覧ください。

1.2は偶数?

山本良和の算数授業 必ず身につけたい算数指導の基礎・基本55 資質・能力を育む授業を実現するための方法

山本良和の算数授業 必ず身につけたい算数指導の基礎・基本55 資質・能力を育む授業を実現するための方法

　「1.2を偶数と言う子どもがいる」や「0は偶数だが，2の倍数ではない」について，子どもたちの理解と関連づけて書かれていました（pp.23-24，「(A)」「(B)」は原文では丸囲みのAとB）．

　算数の学習場面では，「わかる」「できる」「知っている」という状態が混在しています。それは，「算数ができる子ども」「算数がわかっている子ども」「算数を知っている子ども」というふうに子どもに置き換えて表現してみると，それぞれ言葉が異なるように意味合いが違います。この中で，一番表面的で浅い理解を表したものは「算数を知っている子ども」です。
　例えば，低学年でも偶数や奇数という言葉を使う子どもがいます。多くの場合，このような子どもは偶数，奇数という言葉だけを知っている（知識）だけの状態です。だから，「1.2」という小数を見ても，「これは偶数だ」と言うのです。「偶数」という言葉に出会った子どもが自分なりにイメージしたことを結びつけただけの曖昧な状態なので，このような誤った反応が現れます。こういう傾向は，塾などに行って先取り知識を持っている子どもに多くみられます。特に質が悪いのは，その状態でその子ども自身は「自分はわかっている」と思い込んでいるという点です。このような曖昧な子どもの理解を正しい理解へと促すのが学校教育における算数授業の役割の一つだと言えます。
　「1.2」は小数です。偶数は整数を分類したものですから，当然「1.2」は偶数ではありません。小数第一位の「2」だけを見て偶数ととらえてしまっている子どもは，偶数を理解できていないということになります。一方，「1.2は小数だから偶数じゃないよ」と言える子どもは「算数がわかっている子ども」です。学校の算数授業では，このような「わかっている子ども」を育てています。
　余談ですが，｛0，2，4，6，8，10…｝という集合(A)と，｛2，4，6，8，10…｝という集合(B)の違いは「0」の有無です。偶数はどちらでしょうか。
　当然，集合(A)が偶数です。では集合(B)は何でしょうか。こちらは2の倍数です。5年生で倍数の学習をした子どもでも，偶数と2の倍数が同じだと思っている子どもはたくさんいます。このような正確な判断ができることが「算数がわかっている子ども」の姿であるということを改めて確認しておきましょう。

　「1.2」を偶数と判断するのは，「2で割り切れる」あるいは「最後の数が0，2，4，6，8のどれか」を根拠にしているのでしょうか。とはいえ前者だと，1.3も2で割り切れます。後者についても，1.3と等しい\frac{26}{20}は，分母分子とも最後の数が偶数だけど，偶数と見なすわけにはいきません*1。
　上の引用は，子どもたちの発言の一端であるとともに算数教育はかくあるべしという著者の発露であるのを読み取ることができます。ただ，諸手を挙げて賛成というわけにはいかず，深読みしていくと，気になるところもあります。集合の表記は，「｛0，2，4，6，8，10，…｝」と，3点リーダの直前にカンマを打っておきたいです*2し，2箇所に出現する「当然」は，読者（想定読者となる小学校の先生ほか）がきちんと，どうして「当然」なのかを理解しておく必要もあります。「こういう傾向は，塾などに行って先取り知識を持っている子どもに多くみられます」と書くことで，塾などで先取り知識を持ち，かつ「算数ができる子ども」「算数がわかっている子ども」を，対象外とする効果もあります。
　とはいえ「先取り知識」という表現は，算数・数学の違いに気づくのにも有用かもしれません。例えば，「0は2で割り切れる」あるいは「0＝2×0（2×整数）」を根拠にしたり，どこかの本やネット上の情報を根拠に，0も2の倍数だと言う子どもには，「0は0の倍数ですか? 約数ですか?」「0と0の公倍数は? 最小公倍数は?」「\frac14+\frac16を計算するとき，分母は0にしていいの?」などを尋ねることで，0を含めて約数・倍数を扱うにはいろいろな困難が見えてくること，そしてそのデメリットを受け入れてまで，0が2を含め任意の整数の倍数であるとしたとして，算数における意義や実用性はとくに大きくもないことには，注意したいところです。
　同書の「はじめに」では，新しい学習指導要領が告示されたことを踏まえて，不易流行の「不易」のところを整理した本であるとあります。脱稿された平成29年5月よりあとで，新しい『小学校学習指導要領解説算数編』に「このとき0は倍数に含めない」が盛り込まれて公開されたのですが，0は倍数に含めないことは，解説でない学習指導要領からも分かっていた，ということでしょうか。

*1:「偶数＋偶数」「偶数－偶数」「偶数×偶数」はいずれも偶数ですが，「偶数÷偶数」は結果が整数となる場合に限っても，必ずしも偶数になるとは言えません。例えば260÷20＝13により，確かめられます。

*2:偶数・奇数，約数・倍数（0は倍数に含めないことも）を学習したあとで，「偶数を小さいものから5個書きましょう」「2の倍数を小さいものから5個書きましょう」と問い，答えを比べて，0の有無の違いを学ぶという授業があってもよいように思いました。なお，プログラミングにおいて「0，2，4，6，8，…」と書くか，「2，4，6，8，10，…」と書くかは，wikipedia:オリジンと密接に関わるため，小学校のプログラミング学習（の教材研究）でも出現するかもしれません。

新旧の小学校学習指導要領解説算数編から，「端」と「はした」の出現箇所を求める（追記あり）

　新旧の『小学校学習指導要領解説算数編』のPDFファイルを対象に，「端」の語が，前後にどのような表現を伴って出現するかを，取り出してみました。KWIC (keyword in context)形式にしています。
　現行の解説（平成20年6月）はhttp://www.mext.go.jp/a_menu/shotou/new-cs/youryou/syokaisetsu/よりダウンロードできます。以下の2つのファイルをダウンロードしてから，Adobe Acrobat Reader DCで開いて検索し，出現箇所と前後5文字，出現ページ番号を記載しました。

３学年で， 端 数部分の大 (p.36)
の大きさや 端 数部分の大 (p.36)
き，一方の 端 をそろえて (p.44)
て，他方の 端 の位置によ (p.44)
りの個数と 端 数という数 (p.64)
りの個数， 端 数として表 (p.64)
く方法と， 端 数から取っ (p.68)
で，一方の 端 をきちんと (p.71)
，反対側の 端 で，その大 (p.71)
に満たない 端 数がそれぞ (p.80)
とともに， 端 下の処理に (p.90)
　　　　ア 端 数部分の大 (p.111)
踏まえて， 端 数部分の大 (p.112)
多いので， 端 数部分の量 (p.113)
の大きさや 端 数部分の大 (p.114)
の大きさや 端 数部分の大 (p.115)
は，測定で 端 下の数を最 (p.135)
さとその両 端 の角の大き (p.184)
記号化して 端 的に表すこ (p.212)

　新しい解説（平成29年6月）は，http://www.mext.go.jp/a_menu/shotou/new-cs/1387014.htmよりダウンロードできます。以下の2つのファイルを参照し，抽出の方法は上と同じです。

び分数は， 端 数部分の大 (p.44)
き，一方の 端 を揃えて， (p.57)
て，他方の 端 の位置によ (p.57)
い。要点を 端 的に把握す (p.69)
タの特徴を 端 的に捉える (p.69)
りの個数と 端 数という数 (p.79)
りの個数， 端 数として表 (p.80)
０が幾つと 端 数と捉える (p.81)
く方法と， 端 数から取っ (p.86)
は，一方の 端 を揃えるこ (p.90)
，反対側の 端 で長さの大 (p.90)
に満たない 端 数がそれぞ (p.104)
ど，単位の 端 下の処理に (p.121)
　　（ア） 端 数部分の大 (p.147)
踏まえて， 端 数部分の大 (p.148)
・能力は， 端 数部分を表 (p.148)
多いので， 端 数部分の量 (p.148)
の大きさや 端 数部分の大 (p.150)
の大きさや 端 数部分の大 (p.150)
（分や秒の 端 数の付かな (p.164)
は，測定で 端 下の数を最 (p.181)
さとその両 端 の角の大き (p.246)
さとその両 端 の角の大き (p.246)
場合や，極 端 にかけ離れ (p.302)
います。極 端 に多く読ん (p.315)

　新旧に共通して出現するのは「端（単独）」「端数」「端下」「両端」です。単独の「端」は主に1年で，長さの直接比較に関するものです。「端数」は十進位取り記数法や小数・分数で出てきます。「端下」は測定における「はんぱ」の量の扱いで使用されています。「両端」は，三角形の合同や同定に関する事項です。
　そのほか，新しい解説には「端的」「極端」というのも見かけますが，これは新たに作られた領域「D データの活用」の中で出現しています。「極端にかけ離れた値があったりすると」の表記は，現行の中学校学習指導要領解説数学編にもありました。
　新しい解説の算数(2)には，「はした」の語が出現しました（現行の解説には見当たりません）。同様に，出現箇所を書いておきます。

して２ｍの はした があるので (p.188)
に着目し， はした の大きさ， (p.242)


追記：算数用語「はした」について、再び一言 - 身勝手な主張からお越しの方は，以下もご覧ください。

「1あたり×幾つ分」とは，同数累加の乗法表記なのでしょうか?

　上記ツイートについて，回答を試みるなら，次の4点になります。

  • 学習指導要領と解説（新旧とも）から読める、乗法の意味づけの主軸は，2年の「一つ分の大きさ×幾つ分」と5年の「基準にする大きさ×割合」（乗法の意味の拡張）です。なぜ拡張を行うのかというと，累加では，かける数が「幾つ分」という分離量であり，そのままでは，小数の乗法の場面ではうまくいかないからです。
  • 「一つ分の大きさ×幾つ分」の派生が2つあって，一つは「累加の簡潔な表現」，もう一つは「倍」です。いずれも2年で学習しますが，累加は4年の小数×整数でも使用されますし，倍概念は3年のわり算や，（新しい学習指導要領の）4年の「簡単な場合についての割合」とも関わってきます。
  • 「１あたり×幾つ分」は乗法の式で表す方法（演算決定の根拠）で，「同数累加」は計算の方法だ，と区別することもできます。とはいえ，用語はともかくとして同数累加は1年で学習済みなので，5＋5＋5＋5ではなくこれからは5×4と書こうね，という授業の仕方は可能だと思います。
  • 「１あたり」を「一つ分の大きさ」の言い換えとみることも一応できますが，「内包量」（パー書きの量，土台量なども）とすると，意味合いが変わってきます。


　新旧の『小学校学習指導要領解説算数編』のPDFファイルより，「一つ分の大きさ」「幾つ分」「累加」「倍」の出現する箇所を取り出します。現行の解説はhttp://www.mext.go.jp/a_menu/shotou/new-cs/youryou/syokaisetsu/よりダウンロードでき，http://www.mext.go.jp/component/a_menu/education/micro_detail/__icsFiles/afieldfile/2009/06/16/1234931_004_2.pdf#page=27には以下のとおり書かれています。

　ア　乗法が用いられる場合とその意味
　乗法は，一つ分の大きさが決まっているときに，その幾つ分かに当たる大きさを求める場合に用いられる。つまり，同じ数を何回も加える加法，すなわち累加の簡潔な表現として乗法による表現が用いられることになる。また，累加としての乗法の意味は，幾つ分といったのを何倍とみて，一つの大きさの何倍かに当たる大きさを求めることであるといえる。

　新しい解説の起点URLはhttp://www.mext.go.jp/a_menu/shotou/new-cs/1387014.htmです。http://www.mext.go.jp/component/a_menu/education/micro_detail/__icsFiles/afieldfile/2017/07/25/1387017_4_2.pdf#page=39には以下のとおり書かれています。

　ア　知識及び技能
　　（ア）乗法が用いられる場合とその意味
　乗法は，一つ分の大きさが決まっているときに，その幾つ分かに当たる大きさを求める場合に用いられる。
　例えば，「１皿に５個ずつ入ったみかんの４皿分の個数」を求めることについて式で表現することを考える。
（図：省略）
　「５個のまとまり」の４皿分を加法で表現する場合，５＋５＋５＋５と表現することができる。また，各々の皿から１個ずつ数えると，１回の操作で４個数えることができ，全てのみかんを数えるために５回の操作が必要であることから，４＋４＋４＋４＋４という表現も可能ではある。しかし，５個のまとまりをそのまま書き表す方が自然である。そこで，「１皿に５個ずつ入ったみかんの４皿分の個数」を乗法を用いて表そうとして，一つ分の大きさである５を先に書く場合５×４と表す。このように乗法は，同じ数を何回も加える加法，すなわち累加の簡潔な表現とも捉えることができる。言い換えると，（一つ分の大きさ）×（幾つ分）＝（幾つ分かに当たる大きさ）と捉えることができる。
　また乗法は，幾つ分といったことを何倍とみて，一つ分の大きさの何倍かに当たる大きさを求めることであるという意味も，併せて指導する。このときも，一つ分に当たる大きさを先に，倍を表す数を後に表す場合，「２ｍのテープの３倍の長さ」であれば２×３と表す。

　新しい解説では，みかんやテープを用いた場面を取り入れていますが，それを無視して「一つ分の大きさ」「幾つ分」「累加」「倍」に着目すると，言っていることに変化はないと思われます．
　倍概念を2年で学習することや，割合を含め高学年へのつながりについては，啓林館のhttp://www.shinko-keirin.co.jp/keirinkan/sansu/WebHelp/02/page2_16.htmlが最も分かりやすい記述となっています。
　「1あたり×幾つ分」を累加と分離することについては，数学教育協議会の意向もあると思います。遠山啓「6×4，4×6論争にひそむ意味」もその1つです。数教協から離れたところでも，http://www.globaledresources.com/resources/assets/042309_Multiplication_v2.pdfの11枚目上に「累加や，まとめて数えることは，総数（積）を求める方法である。」*1とあります．この項目が，「かけ算の式は，それと数の等しい，決まった状況を表す。」*2の下位となっていることからも，かけ算の式で表すことが主，計算で求めることが従となっているのが見て取れます。
　最後に「1あたり」を「内包量」に読み替えるとどうなるかですが，「1あたり×幾つ分」によって，その結果は被乗数・除数のいずれとも異なる種類の量となるので，これを「積」のかけ算と解釈することができます。数教協のスタンスを，その外の人が整理したものが，『数学教育学研究ハンドブック』*3より読めます*4．以下の2つはp.73からです。

　演算の意味（演算決定）についての議論は，様々な立場から提案がされている。
　特に，乗法の意味には，「同数累加」，「量×量」，「基準量×割合」の3つの立場がある。

　中原(1961)は，分数の乗除は，量×量，量÷量とて，量の関係として扱うべきであると主張し，乗法を累加で定義して，後に倍概念に拡張する立場を批判している。加法と乗法は本来性質の違う演算として導入すべきであると主張する。乗法は2つの量の「積(product)」として捉え，「倍(multiple)」ではないとしている。この立場から乗法を次の3つの概念で分類している。
(1) 2m×3＝6m
(2) 2m×3m＝6m^2
(3) 2m/秒×3秒＝6m
　(1)は「倍」で，2つの量の比較する場合に生まれる概念であり，拡張によって小数倍，分数倍へと発展する。(2)と(3)は「積」であり，(2)は「外延量×外延量」で面積のような二元的な量，(3)は「内包量×外延量」で速さなどである。この「積」の概念が乗法演算の本質であるとしている。

　今の算数では，式に単位を付けないのが慣例ですので，上記(1)～(3)の表記は，2×3という式の解釈の仕方と見ることができます。連続量を用いていますが，分離量でも考えることができ，新しい解説のみかんの場面について，「5個×4（＝5個＋5個＋5個＋5個）＝20個」が「1つ分の数×いくつ分」に，「5個/皿×4皿＝20個」が「１あたり×幾つ分」に，それぞれ関連づけられます。この分類では，新しい解説で例示されたみかんの場面もテープの場面も，「倍」となりますし，「１あたり×幾つ分」は累加で解釈できないことになります（それを踏まえた上での「積」と言えます）。
　ただし，『数学教育学研究ハンドブック』では，以下の内容が，乗法の意味に関する結論となっています(pp.74-75)。

　これらの研究成果から，乗法・除法の意味づけにおいては，数学的な考え方の育成を目指す立場からは，割合による意味づけに教育的な価値がある。これは，整数は同数累加で導入し，乗数が小数になった段階で同数累加では意味づけられなくなる。そこで，被乗数，乗数の意味を（基準量）×（割合）と拡張し，これまでの整数の場合と同様に用いることができるようにすることである。数学的な考え方を育成するためには，意味の拡張は重要な指導の場となってくる。
　この意味づけにおける課題は，児童の実態として，割合を捉えることの難しさが挙げられる。整数の乗法・除法を扱う中で割合の見方をどの学習でどのような方法で導入するかを明確にする必要がある。また，整数÷整数の包含除の場面で整数倍，小数倍を扱う指導と割合との関連を，より一層カリキュラムの上で明らかにする必要がある。
　一方，意味の拡張を意図しない立場では，乗法の意味づけは，（内包量）×（外延量）になる。乗数を外延量とすることで，整数でも小数でも意味づけは変わらないことになる。
　この意味づけの課題は，乗法の導入段階で内包量の見方を児童ができるかということである。例えば，みかんが3こある場面で，これを3こ/皿という内包量として見るのは児童にとって難しいことである。また，数学的な考え方と関わった意味の拡張などの見方をどのように扱うかを明らかにする必要がある。

　とはいうものの，「１あたり」も「内包量」も，パー書きの単位も，小学校算数の学習指導要領および解説には出現しません。「１あたり」に近いのは，「単位量当たりの大きさ」ですが，その学習は5年です*5。
　2年で学習する，かけ算の言葉の式としては，「多くの教科書で採用している」と断った上で「1つ分の数×いくつ分」と書くのが無難ではないか，とも思います。
　なお，冒頭のツイートの1つ前*6について，学習指導要領やその解説の作成・改訂のプロセスよりも，東京新聞（中日新聞）に出された記事の経緯の方が気になっています。とくにその発端に関して，ネットの議論を記者が読んだというよりは，誰かが，記事にするよう持ちかけたのではないかと思わずにいられないのです。

*1:原文は"Repeated addition and skip counting are ways to find the total (product)."

*2:原文は"Multiplication sentences describe equal set situations."

*3:isbn:9784491026268

*4:執筆者は中村享史。関連：http://d.hatena.ne.jp/takehikom/20161122/1479743916

*5:人口密度や速さなど，単位量当たりの大きさは，わり算によって求めるのに対し，「3こ/皿」などの「1あたり」は，かけ算の導入で（わり算を陽に出さずに）使用する，という違いもあります。

*6:https://twitter.com/metameta007/status/892750423680929793