〔4×100m,-60kgに+100kgも合わせてご覧ください。〕
このツイートを目にして,先月見たものの,記事にする機会を失っていた,かけ算の式を思い出しました.Gmailで検索をしたところ,メールに残っていましたが,Webで誰でも読めるところを見つけましたので紹介します.
ぐるなび会員に登録(ログイン)して、「スーパーらくらく幹事さん」または「プラン予約(とくとくプラン)」でお店をWEB予約、あとはお店のぐるなびタッチ読み取り機にケータイでチェックインすると、来店人数×100ポイントがもらえます。ぐるなびでお店を予約して、ポイントでお得に宴会を楽しもう!さらにプレミアム会員なら予約ポイントが2倍(来店人数×200ポイント)がもらえます。
この中の「来店人数×100ポイント」という,言葉と数量の交じった式については,来店人数を「かけられる数」に,そして100ポイントのほうを「かける数」に,それぞれ対応づけることができます.例えば,来店人数が6名だとすると,合計ポイントは6×100で600ポイントとなりますが,このときの「×100」は,100倍という意味ではなく---もしそうなら600人になってしまう!---,来店人数を合計ポイントに変換する作用素となります.これは,6人×100ポイント/人=600ポイント と表すことができます.
また違った,「来店人数×100ポイント」への解釈を与えることもできます.来店人数を「かける数」,100ポイントを「かけられる数」とします.そして,積を求める際にかける数のほうは,「人」の意味を失い,ポイントを人数倍する,という考え方です.上と比較するなら,6×100ポイント=600ポイント という式で表されます.
今回見てきた「来店人数×100ポイント」と,ツイートの「4×100m」は,ともにかけ算の結果が,乗算記号の左の「〜人」ではなく,右の数量と同じ種類(単位が同じ)である,という共通点があります.しかし違いもあって,「4×100m」では,4をかけられる数と見なす人はいないと思われます.
関連:
乗法の場面、「1ふくろにミカンが3こずつ入っています。5ふくろでは、ミカンは何こでしょう。」は、3×5と立式される。立式は、「1つ分の数×いくつ分=全体の数」とまとめられ、それぞれ被乗数、乗数という。ところで、「オリンピックの400メートルリレー」や「このDVDは16倍速で記録できる」、「xのk倍は」の式は、どのように表わされるであろうか。それぞれ、一般的には「4×100mリレー」、「16×」、「kx」と表される。被乗数と乗数の位置が教科書の書き方と逆になっていることに気付くであろう。この例から分かるように、乗法では、数の位置ではなく、数が意味する内容に注目して、どの数が1つ分の数であるか、いくつ分はどの数かをしっかりと読み取ることが大切である。第2学年や第3学年では、読み取った数を、「1つ分の数×いくつ分=全体の数」と表現できることが重要であり、逆に、この立式ができているかで、数の読み取りができているかを判断できる。しかし、高学年になり、乗法では交換法則が成り立つことや外国での立式を知り、数の意味をしっかり理解できていれば、必ずしも第2学年で学んだ順序で立式することを強制しなくてもよい。
(『小学校指導法 算数 (教科指導法シリーズ)』pp.91-92; 転載元)
仕事で国外に行く機会が多くなって,ものすごく強く感じることは,算数の言葉としての式は世界共通で,地球の裏側のブラジルに行っても,2+3と書けばみんな5と書いてくれる。あの数字は世界共通ですから。3×2は地球の裏側に言っても6です。
ブラジルに行ったときに6の目のサイコロを見せて,「サイコロの目の数はいくつですか」と言うと,みんな「6」と言った。「どうして6と考えたの」と尋ねるとある子が出てきて,「3×2」と書いたんです。これを3×2と見たわけを聞きました。私がどうしてそんなことを聞いたかというと,式の後ろに潜んでいる感覚は,日本語圏以外では普通意味が逆です。3×2と言えば,日本では「3個のかたまりが2個ある」という意味ですが,英語圏も中国語圏もみんな「3個ありますよ,2つのものが」という意味です。
一番わかりやすい例は,陸上競技で4×100mリレーという表示がありますね。日本で正しく勉強している子なら,4mを100人で走ると言うことになる。でも,誰もそう解釈しませんね。これは世界共通で4人で走りますよ,100mずつを,という意味の表示です。日本とは式の意味が逆なんです。だから,3×2とブラジルの子が書いたから,あえてちゃんと聞いてみたいと思ったんですね。そうしたら,はじめに出てきて説明した子は3個ずつのかたまりを作ってそれが2つ分と言いました。おやっ,これは日本と同じだぞと思っていると,他の仲間みんなが違う違うと言うのです。要するに間違っていたのです。どこの国も同じですね,間違える子がいるのは。本当は2個のかたまりが3個分だと別の子が説明してくれました。
このように式の裏に隠れている文化は違います。
(『坪田耕三の算数授業のつくり方 (プレミアム講座ライブ)』p.138; 転載元
15セントのケーキを4個
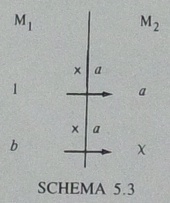
(略)「1個15セントのケーキを4個買います.いくらになりますか」という問題を考えます.aを15セント,bを4個とします.xは60セントであって,60個ではありませんね.SCHEMA 5.2, 同5.3とも,M1はケーキの個数の量空間,M2は金額の量空間です.
SCHEMA 5.2の考え方では,M1で1個から4個になるのを「×b」とします.同じ量空間における「b倍」を,M2へ適用することで,a=15セントの「4倍」がx=60セントになるわけです.
このとき,「×b」のbは,もはや「4個」ではありません.あえて量という言葉を使うなら,無次元量です.
SCHEMA 5.3は,横に見る関係といえます.1個だと15セント,という関係を「×a」で表します.そうすると,4個だと,「×15」とするので60セントです.
ちょっと注意したいのは,この場面での「×15」は,数だけ見れば15倍ですが,実際には,M1という量空間からM2という量空間へ変換しています.あるいは,「×a」が,M1とM2という2つの異なる量空間の仲立ちをしている,と考えることもできます.
このとき,「×a」のaは,これまた「15セント」ではなく,「15セント/個」とするほうが,より適切でしょう.言葉にすると,「1個(あたり)15セント」です.
量空間は,数学的に定義しているわけではなく,同じ性質の集まりという程度なのでしょう.その一方で,数学的な取り扱いでの「量」だと,連続量が対象とせざるを得ないところ,Vergnaudの議論では,ケーキの数や金額など,分離量も視野に入れています.