周りの長さ～算数授業研究より

• 大野桂: 「活動」に問題解決の方略と数学的な見方・考え方が表出する, 算数授業研究, 東洋館出版社, Vol.121, pp.50-51 (2019).

算数授業研究 Vol.121 論究XIV: 算数と「活動」

　見開きの文章は，タイトル・小見出しを別にして「教科書6者全てに掲載されている，4年「ともなって変わる2つの量」の問題である。」から始まります。どんな問題なのかについては，以下をご覧ください。

• 段数×４＝周りの長さ
• https://www.slideshare.net/takehikom/23-32-123835241/73

　『小学校学習指導要領算数編』の該当箇所は，現在，http://www.mext.go.jp/component/a_menu/education/micro_detail/__icsFiles/afieldfile/2019/03/18/1387017_004.pdf#page=236より見ることができます。

　大野氏の解説では，当初は正方形の色板だったのが，途中から棒*1に置き換えています。そうすると，棒のスライドが可能となり，周りの長さ（棒の本数）が「段数×4」「4×段数」と表せることを確認しています。

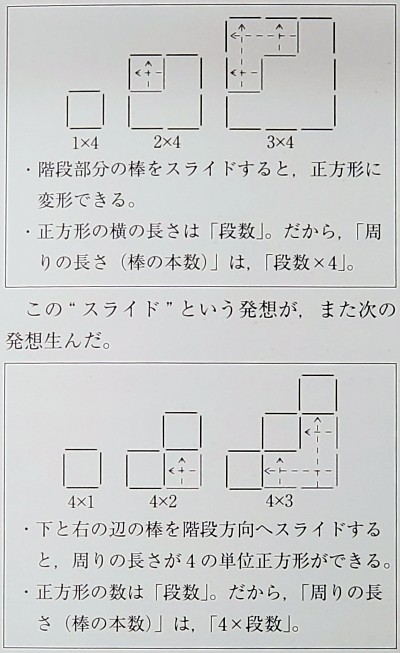
　「周りの長さ＝段数×4」「周りの長さ＝4×段数」となる，2つの式において，乗法の交換法則は直接的には使用していません。これについて，帰納的な考え・演繹的な考えが，背景にあるように思います。掲載された図としては（あるいは授業で），棒の数が変わらないよう形を変更するのは，段数が小さいものに限られますが，10段や100段ともなると，棒を配置することなく，同様の操作で，1辺が棒の10本分の正方形や，棒4本による正方形を100個，作ることができると考えます．棒1本の長さが1cmであれば，100段の場合の周りの長さは，100×4でも4×100でもよく，答えは100cmというわけです。
　ここまでは，この階段状の周りの長さという問題に特化した話です。「ともなって変わる2つの量」の学習を通じて期待される，数学的な見方・考え方は，以下の対応付けではないかと考えています。

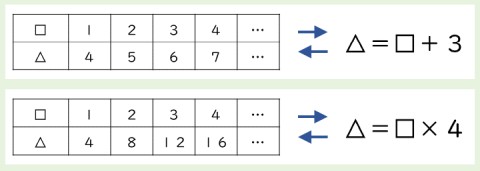
　表の上の段と下の段は，異なる種類の量であっても，それぞれの表のような対応関係が得られるのであれば，「△＝□＋3」「△＝□×4」といった式で表すことができる，ということです。表の上と下には区別があり，上は「独立変数」，下は「従属変数」となります（それらの用語を小学校で教えるわけではありませんが）。「3」「4」は具体的な場面に応じて決まる定数であり，次期解説では三角形の数と周りの長さを「□＋2＝△」の等式で表しています。
　表づくりは，同種の2つの数量の関係にも，対応しています。啓林館と教育出版の，4年下の算数教科書を見ると，同じ長さの18本の棒を使う，18cmの紐をジオボードに引っかけるという方法で，長方形*2を作るときの，縦と横の長さを表にしています。縦の長さまたは本数を○，横の長さまたは本数を△として，「○＋△＝9」を得ます*3。教育出版のほうでは鶴亀算を表で解く方法*4も載せています。

*1:「マッチ棒パズル」の応用にも見えます。とはいえ算数の授業で，子どもたちが各自，それなりの本数のマッチ棒を持参して，配置したり並べ替えたりするのは，現実的ではありません。

*2:ジオボードの格子点の間隔を1cmとし，紐の重複がなければ，正方形（1辺の長さは4.5cm）になることはありません。

*3:この場合，独立変数・従属変数といった区別をせず，「縦の長さと横の長さの和は9」となります。

*4:『算数再入門』isbn:9784121019424ではpp.177-179に「小学校4年生の解き方（表で解く）」を取り上げています。