かけ算の順序の昔話

算数教育について気楽に書いていきます。

「被乗数と乗数の順序」について

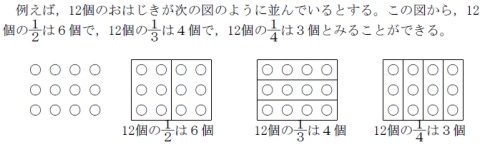
　「被乗数と乗数の順序」を，算数教育（ネットの風評ではなく）の流れの中で理解するには，現行（2008年公開）およびこれから（2017年公開）の『小学校学習指導要領解説算数編』のあいだ，2011年に出版された『新しい学びを拓く算数科授業の理論と実践』を読んでおきたいところです。


　『小学校学習指導要領解説算数編』（平成29年6月）のPDFファイル*1を見ると，p.114に3回，「被乗数と乗数の順序」が出現します。段落は次のとおりです。

　ここで述べた被乗数と乗数の順序は，「一つ分の大きさの幾つ分かに当たる大きさを求める」という日常生活などの問題の場面を式で表現する場合に大切にすべきことである。一方，乗法の計算の結果を求める場合には，交換法則を必要に応じて活用し，被乗数と乗数を逆にして計算してもよい。*2

　式を読み取る指導に際しては，例えば，3×5の式から，「プリンが3個ずつ入ったパックが5パックあります。プリンは全部で何個ありますか。」という問題をつくることができる。このとき，上で述べた被乗数と乗数の順序が，この場面の表現において本質的な役割を果たしていることに注意が必要である。「プリンが5個ずつ入ったパックが3パックあります。プリンは全部で幾つありますか。」という場面との対置によって，被乗数と乗数の順序に関する約束が必要であることやそのよさを児童に気付かせたい。

　Googleで"被乗数と乗数の順序"を検索したところ，2014年に，別々の3つのところで，使われているのが確認できました。

その2. 《被乗数と乗数の順序》
次に見ておきたいのは，かけ算の式を「かけられる数×かける数」で表すか，「かける数×かけられる数」で表すかです．
この場合，かけ算の答えと同じ種類の量になるほうを「かけられる数（被乗数）」，他方を「かける数（乗数）」とします．なお，面積を含む「量の積」や，アレイの計数は，対象外となります．
メールで「3コマ×5人＝15コマ」と書いて送れば，「3（コマ）」がかけられる数，「5（人）」がかける数です．あるレシートに「17個 X 単105」と打たれていれば，「17（個）」はかける数，「単105」は単価が105円とみなし，これがかけられる数となります．
これに由来する順序を，《被乗数と乗数の順序》と呼ぶことにします．

Description　日本語: かけ算の順序に関して、，乗数と被乗数の順序が加算減算と異なることの説明

（３）被乗数4×乗数3＝被乗数3×乗数4
これが、文科省の理解であった。
　被乗数と乗数の区別について、×の左を被乗数、右を乗数とするのは、明治時代に西洋から教わったときの西洋の主流の理解がそうだったからであり、現在の西洋の主流は逆になっても、日本では教わったときの順序を守っているわけである。
　つまり、数字4と3の順序は入れ替わっても、被乗数と乗数の順序は入れ替わらないのである。

　2014年の上記の3件は，依拠するものが異なっています。最初と最後のブログ記事は，それぞれ本文中に書かれています。2番目のgifですが，状況としてはwikipedia:かけ算の順序問題に追加するための画像を試作し，日の目を見なかったと思われます。
　もう少し補足すると，英文的演算では「2×」が左に来ることについては，古くから指摘があり，1968年のhttp://ci.nii.ac.jp/naid/110003849391の文献のほか，『算数・数学教育つれづれ草』*3p.46に書かれている，「5円の品3個の代金の立式は，3×5ではダメなのか」の論争が，昭和40年（1965年）ごろに湧き起こったこととも関連します。
　ここまで『小学校学習指導要領解説算数編』を含め，ネットで読める情報ばかりでした。ですが，2011年に出版された中にも，「被乗数と乗数の順序」を明記しているものがありました。

新しい学びを拓く算数科授業の理論と実践 (MINERVA21世紀教科教育講座)

新しい学びを拓く算数科授業の理論と実践 (MINERVA21世紀教科教育講座)

　出現するのはp.113です。

　乗法の数学的定義についても，集合の要素の数という観点からの定義と，順序という観点からの定義がある。
　算数科では，整数の乗法は，一つ分の大きさが決まっているときに，その幾つ分かにあたる当たる大きさを求めるという場面で導入される。整数の世界では，その値を求めるためには，同数累加を行うことになる。つまり，乗法は同数累加の簡潔な表現として用いられることになる。この定義では，3×4＝3＋3＋3＋3，4×3＝4＋4＋4となる。つまり，被乗数と乗数の順序に意味がある。また，交換法則（a×b＝b×a）やa×（b＋1）＝a×b＋aが成り立つことにも気づかせたい。例えば3×5の場合，3を5個足す代わりに，3を4個足したもの（3×4）に3を1個加えればよい。つまり，3×5＝3×4＋3となる。この性質を活用して1位数同士の乗法を考えていく（乗法九九の構成）。なお，平成20年改訂の学習指導要領においては，これらの乗法九九の構成の延長として，被乗数や乗数が12程度までの乗法を扱うこととなっている。

　ここの「被乗数と乗数の順序に意味がある」について，2種類の解釈ができます。一つは，「3×4＝3＋3＋3＋3であり，4×3＝4＋4＋4なのだ」と，被乗数と乗数の順序に，意味が定められている，というものです。
　もう一つの解釈では，「に意味がある」を「は重要だ」と置き換えます．英語でぴったりの単語があり，自動詞のmatterです。http://books.google.co.jp/books?id=2NX4I6mekq8C&pg=PA3より読める授業で，先生が"Eddie says that order does matter"と言うシーンがあります*4。
　「意味」はともあれ，上記の「算数科では」から始まる段落は，新しい学習指導要領および解説の記述にも適合します。時系列としては，2008年に現行の『小学校学習指導要領解説算数編』が公開・発行され，それをもとに『新しい学びを拓く算数科授業の理論と実践』で解説がなされ，「意味がある」が「本質的な役割を果たしている」や「約束が必要である」に置き換えられて，2017年6月，新しい学習指導要領に基づく『小学校学習指導要領解説算数編』に記載された，という流れを見ることができます。
　なお，上記引用を含む第6章第1節の執筆者は清水紀宏氏です。福岡教育大学教授で，日本文教出版の平成27年度版『小学算数』の著作者にも，名前が載っています。
　「順序」の言葉は出現しませんが，次の本も見ておきます。

「小学算術」の研究

「小学算術」の研究

　著者の高木佐加枝は，昭和10年からの「緑表紙教科書」の編纂に携わった人です．「緑表紙教科書」では，九九の学習をそれまでの乗数先唱（3×4＝12は「しさんじゅうに」）から被乗数先唱（3×4＝12は「さんしじゅうに」）に改めました。その根拠が，『「小学算術」の研究』pp.246-247に記されていました。

a. 各段の九九を被乗数を一定にして纏めることにすると，この一定な数を冒頭に呼ぶ方が都合がよい。筆算の掛算では，乗数先唱を本体とするが，これは後に指導することで，九九構成の最初においては，被乗数先唱で九九を覚えさせることが，児童心理に叶っている。
b. 国語は，「5円の色紙を8枚」「3を4倍する」というように，被乗数を先にする言い方である．
c. 式に表す場合も　5円×8　というように，被乗数を先に書くのを常とするから，被乗数先唱の方が都合がよい。

　最後の項目の「5円×8」も興味深いところです。「5円×8枚」ではありませんし，積は40円です。とはいえ今の算数では，式に単位を付けず，「5円の切手を8まい買いました。ぜんぶでいくらですか」という文章題には，式は5×8＝40，答えは40円と書くことが期待されます。

　お知らせ：本記事の内容を手直しし，かけ算の「順序」について（2017.12）に取り入れました。合わせてご覧ください。

*1:http://www.mext.go.jp/a_menu/shotou/new-cs/1387014.htm

*2:第1文は，結城浩『プログラマの数学』でかかれた図（http://d.hatena.ne.jp/takehikom/20150128/1422391025）を使うと，「別世界の問題へ変換する」に関するもので，第2文は「別世界で解く」です。交換法則が立式の段階で適用できないのは，それぞれのステップで使えるものが異なるからと言えます。

*3:isbn:9784491026183

*4:ただし乗法の交換法則の学習ということもあり，"the answer is the same no matter which number goes first."や"I don't think it matters what order the numbers are in."のように，否定語を含む文の中にも出現します。私訳はhttp://d.hatena.ne.jp/takehikom/20150822/1440184614をご覧ください。

中央公論2015年12月号の，“掛け算の順序問題”を含む対談

　この記事の趣旨は，小学校を通してかけ算がどのように学習されているかをきちんと認識することなく，「かけ算の順序問題」が教育批判のための道具として手軽に使われているなあという，残念な気持ちの表明にあります。

　中央公論2015年12月号掲載とのこと．知ったきっかけはhttp://d.hatena.ne.jp/samakita/20170315/p1です。対談の途中に「掛け算の順序問題」が出てきます。

川端「今日、是非お話ししたいと思っていたのが、小学校の“掛け算の順序問題”です。“1×2”も“2×1”も答えは同じですよね。しかし、（※）これを『問題文の順序通りの式で計算しないと不正解にする』という動きが小学校であるんです。例えば、『脚が2本の鶏が3羽いた時、脚の数は全部で何本でしょう？』という問題なら、（※）“2×3＝6”は正解で、“3×2＝6”を不正解にするという具合です。不正解とされた子供の保護者が驚いて、毎年必ず議論になるんです」
左巻「『どちらか一方の式しか正解にしない』というのは、数学的な思考とは言えないですね」
川端「掛け算を初めて習う小学生にわかり易いように、『2本の脚×3羽だから6本でしょう』と説明をするのはわかりますが、それを小学5～6年生になっても『片方の式しか認めない』という教育が行われているのは変だと思うんです」
左巻「教師が使う指導書に、『こう教えるように』と書いてある場合があるんですよ。教科書は検定を通らないと使えませんが、指導書は検定を受けないので、何を書いても許されるんです」
川端「少なくとも、教科書会社は『小学生の間は順序を固定しなければいけない』と考えている訳ですね。これはもう、現場の教師レべルではどうしようもなくて、教材として使われるドリルやワーク等も、正解を一方に固定するものが使われている訳です。それくらい深く浸透している。わからないのは、『こうした非合理的な信念はどこから来るのか？』ということです。結局、中学生になればどっちでも正解になります。というか、そんなことは先生も気にしなくなる」
左巻「昔は、そんな教え方は無かったと思います。マイナーな指導法が、いつの間にか拡散していったのかもしれません。掛け算をイメージし易く教える導入場面はあってもいいと思いますが、順序をずっと固定化・強制して、逆に答えると『掛け算の意味を理解していない』と×にするのは、直ぐに止めてほしいですね」

　2度出現する「（※）」については，ページの終わりに注釈が入っています。

（※）　混乱を招く言い方なので、深くお詫びします。書き直すとすれば、「文章題の計算をする時、決められた順序で式を立てないと不正解にするという動きが小学校であるんです」「うっかり出てきた順に“3×2＝6”と書くと不正解。“2×3＝6”が正解という具合です」。個人でとりいそぎできる訂正としてここに掲示しておきます。
http://blog.goo.ne.jp/kwbthrt/e/d3d063f9ae6b16474acbe3cc050648dc

　リンク先を読みました。書き直し案があります。

書き直すとすれば、
*****
川端　今日、ぜひお話ししたいと思っていたのが、小学校の「かけ算の順序問題」です。一×二も二×一も答えは同じですよね。しかし、文章題の計算をする時、決められた順序で式を立てないと不正解にするという動きが小学校であるんです。
例えば、「三羽の鶏がいます。鶏の脚は二本です。脚の数は全部で何本でしょう」という問題で、うっかり出てきた順に三×二＝六と書くと不正解。二×三＝六が正解という具合です。不正解とされた子どもの保護者が驚いて、毎年必ず議論になるんです。
*****
これ、二段落目も、問題を際立たせるために変えてます。

　ここまで見た上で，関連しそうなものと対比していきます。
　まず，対談中の「問題文の順序通りの式で計算しないと不正解にする」について，思い浮かぶのは以下の本と，増刷による書き換えです。

江戸しぐさの正体 教育をむしばむ偽りの伝統 (星海社新書)

江戸しぐさの正体 教育をむしばむ偽りの伝統 (星海社新書)

　2014年のこの件が，2015年の中央公論の対談でも同様に起こっているというのは，小学校を通してかけ算がどのように学習されているかをきちんと認識することなく，「かけ算の順序問題」が教育批判のための道具として手軽に使われていると，思えてなりません．
　『江戸しぐさの正体』では「交換法則」を持ち出し，また上記対談ではこの語の代わりに「“1×2”も“2×1”も答えは同じですよね」という発言が見られます。
　これもまた，国内外の算数教育の状況を把握していないと言わざるを得ません。それらの式を使うなら，「1×2と2×1，答えは同じでも意味が違う」です。国内でいうと，東京書籍の教科書の例があります。

f:id:takehikoMultiply:20170627051603j:plain

　国外の授業については，日本語非ネイティブの教授が紹介しています。

　この文献に見る，イランの授業では，「16を3でかける」と「3を16でかける」の意味の違いを，ある生徒が発表し，そこで先生がみんなに拍手を促すシーンがあります。アメリカの授業の事例でも，原文となるhttp://books.google.co.jp/books?id=2NX4I6mekq8C&pg=PA3を読むと，「5個入りのリンゴが2袋」と「2個入りのリンゴが5袋」を言う生徒の発表を，先生は肯定的に取り上げています。交換法則に関連する「答えは同じ」を指摘する生徒に対しては，「2つの式が違った場面を表すのに使えないって言うのですか?」と先生が質問をしていており対照的です。
　最後に，中央公論の対談にも，川端裕人氏による書き直しにも見られる，「という動きが小学校であるんです」について，いつからその種の指導（また指導を意図した出題）がなされているかが無視されています。書き直された「三羽の鶏がいます。鶏の脚は二本です。脚の数は全部で何本でしょう」について，同種の出題を以下にて整理しています。

　意図されているのが分かるのは，1941年の「カズノホン（水色表紙教科書）」です。より具体的な指導は，1951年の小学校学習指導要領算数科編（試案）にあります。また1957年に刊行された『算数科の教育心理』という本では，当時かけ算を学ぶ3年生では，かけられる数とかける数を反対に書くのは指導の対象となっています。
　ただし，『算数科の教育心理』において，45名で4回ずつイスを運ぶ場面で，4×45のほか45×4でも正解となることを，子どもたちに見つけさせています。4年生の指導例です。この種の授業が，これまで（現行の学習指導要領や算数教科書のもとで）なされていたわけではありませんが，トランプ配りや，Vergnaudの関数関係などととも関連しており，新しい『小学校学習指導要領解説算数編』でもその一部が取り入れられています。
　「それを小学5～6年生になっても『片方の式しか認めない』」でないことを含む事例を，以下にて紹介しています。

　小学校を通じて，かけ算がどのように学習されているかをきちんと認識することなく論じられる状況を，残念に思います。

新しい学習指導要領では，割合を4年で学ぶ

　『小学校学習指導要領解説算数編』（平成29年6月）のPDFファイル*1を読み，そこでは（すなわち平成32年度からは），割合を4年で学習することになるのを確認しました。
　「算数(1)」のファイル，すなわち各学年の説明より前の文書の中から，主だった箇所を抜き出します。

(p.61)
f:id:takehikoMultiply:20170626055656j:plain

(pp.63-64)
二つの数量の関係と別の二つの数量の関係とを割合を用いて比べること
　二つの数量の関係と別の二つの数量の関係を比べるとは，A，Bという二つの数量の関係と，C，Dという二つの数量の関係どうしを比べることである。ここで，比べ方には大きく分けて，差を用いる場合と割合を用いる場合があると考えられる。「A君はBさんより3歳年上である。CさんはD君より5歳年上である。どちらの方が年齢差があるか。」では，AとBの関係とCとDの関係という二つの数量の関係どうしを，差でみて比べている。
　一方，比べる対象や目的によって，割合でみて比べる場合がある。割合でみるとは，二つの数量を，個々の数量ではなく，数量の間の乗法的な関係で見ていくことである。例えば，全体の中で部分が占める大きさについての関係どうしや，部分と部分の大きさの関係どうしを比べる場合は，割合でみていく。「シュートのうまさ」を，「シュートした数」と「入った数」という全体と部分の関係に着目して比べる場合などである。また，速さを比べる場合のように，距離と時間などの異種の量についての関係どうしを比べる場合は，差で比べることには意味がないため，割合でみていくことになる。
　二つの数量の関係どうしを割合でみて比べる際は，二つの数量の間の比例の関係を前提としている。二つの数量の関係と別の二つの数量との関係が同じ割合，あるいは，同じ比であることは，問題にしている二つの数量について，比例の関係が成り立つことが前提となっている。上述の「シュートのうまさ」の例で言うと，0.6の割合で入る「うまさ」というのは，10回中6回入る，20回中12回入る，30回中18回入る…などを，「同じうまさ」という関係としてみていることを表している。また，二つの液体AとBを2:3の比で混ぜ合わせてできる「液体の濃さ」も同様である。そして，この前提に基づいて，数量の関係どうしを比べたり，知りたい数量の大きさを求めたりしている。このように，割合では，個々の数量そのものではなく，比例関係にある異なる数量を全て含めて，同じ関係としてみている点が特徴である。

(p.64)
二つの数量の関係に着目すること
　これは，日常の事象において，割合でみてよいかを判断し，二つの数量の関係に着目することである。
　第4学年では，日常の事象において，比べる対象を明確にし，比べるために必要な二つの数量を，割合でみてよいかを判断する。そして，一方を基準量としたときに，他方の数量である比較量がどれだけに相当するかという数量の関係に着目する。第4学年では特に，基準量を1とみたときに，比較量が，基準量に対する割合として2，3，4などの整数で表される場合について扱う。(略)

(pp.64-65)
数量の関係どうしを比べること
　これは，図や式を用いて数量の関係を表したり，表された関係を読み取ったりしていくことで，割合や比を用いて数量の関係どうしを比べることである。
　第4学年では，日常生活の場面で，二つの数量の組について，基準量をそれぞれ決め，基準量を1とみたときに，比較量がどれだけに当たるかを，図や式で表す。そして，個々の数量の大きさと混同することなく，割合を用いて，数量の関係どうしを比べ，考察していく。(略)

(p.65)
二つの数量の関係の特徴を基に，日常生活に生かすこと
　これは，二つの数量の関係どうしを割合や比で比べた結果を，日常生活での問題の解決に生かしていくことである。
　第4学年では，基準量の異なる二つの数量の関係どうしを，2，3，4などの整数で表される割合を用いて比べる場面で，得られた割合の大小から判断をしたり，割合を用いて計算をした結果から問題を解決したりする。(略)

　「算数(2)」で第4学年を見ていくと，「乗数や除数が整数である場合の小数の乗法及び除法の計算ができること」(p.189)のところで，「除法の意味は，乗法の逆で，割合を求める場合と基準にする大きさを求める場合で説明できる」と書き，その次の段落の「6mは4mの何倍かを求める場面」が，割合を求めるように読めます。ただしこの節では，6÷4＝1.5によって得られる1.5倍が割合となることを明言していません。A（数と計算）の領域です。
　同じ学年のC（変化と関係）の領域では，「簡単な場合について，ある二つの数量の関係と別の二つの数量の関係とを比べる場合に割合を用いる場合があることを知ること。」が（解説のつかない）学習指導要領に入っていることもあり，詳しく解説されています。ここで「簡単な場合」とは，上で引用したとおり，「基準量を1とみたときに，比較量が，基準量に対する割合として2，3，4などの整数で表される場合」です。例題としては「ある店で，トマトとミニトマトを値上げしました。トマトは１個100円が200円に，ミニトマトは１個50円が150円になりました。トマトやミニトマトではどちらがより多く値上がりしたといえますか。」(p.214)や「平ゴムAと平ゴムBがあります。平ゴムAは，10cmが30cmまで伸びます。平ゴムBは，80cmが160cmまで伸びます。どちらがよく伸びるゴムといえますか。」(p.215)が書かれています。
　2つの領域で，わり算によって得られる値が異なります。Aの領域では，「整数÷整数＝小数」を行い，ある場面ではその商（小数）が割合に対応します。Cの領域では，「整数÷整数＝2または3または4」です。割合を計算するだけでなく，「乗法的な関係でみてよいかを判断」することや，「図や式を用いて数量の関係どうしを割合で比べること」などが，Cの領域では要請されています。
　ただし，解説には明記されていませんが，共通点もあります。これらのわり算は，「割合の第1用法」であり*2，かつ，整数÷整数による計算に限られます。
　演算の対象を小数にまで広げるとともに，意味の拡張を行い，p：割合，B：基準量，A：比較量として，「p＝A÷B」「A＝B×p」「B＝A÷p」の場面でも適切に式を立てて答えを求められるようになるのは，5年の学習事項です。なお，4年では，「10mは4mを1とすると2.5にあたる」(p.188)などにより，小数を用いた倍を学習しますが，4×2.5＝10といった式は対象外です。
　ここまでのことは，日本学術会議 数理科学委員会 数学教育分科会が昨年公表した初等中等教育における算数・数学教育の改善についての提言の，pp.6-7に書かれた「改善の具体案」が反映されたものとなっています。長くなりますが抜き出します。

(1) 小学校
① 「割合」の背景にある考えの位置づけ
　割合の意味の理解については学力調査などの結果から課題があることが明らかである。割合の扱いは、第5学年の百分率や異種の2つの量の割合のときだけでなく、乗法・除法の意味付けや分数で表記された数量の解釈などでも用いられている。それらの系統を明示するとともに、特に、以下の位置づけについて、改善すべきある。
ア 分数倍、小数倍の位置づけ
　小数倍、分数倍を系統的な観点から位置づけるべきである。
　例えば、5mと2mのテープを比べるとき、「差で3mの違いとみる見方」以外に、「2mを1とすると5ｍは2.5倍（5/2）となり、5mを1とすると2mは0.4倍（2/5）となる見方」があり、後者を除法の系統の中で明らかにすべきである。また、分数の指導において、「8の1/2は4」「6の1/3は2」などの2つの数の関係を分数で表すことも扱うべきである。小数の指導においても同様であり、小数と分数を関連させて、同じ数を表す異なる表記であることを強調すべきである。
イ 演算の意味指導の位置づけ
　乗数や除数が整数から小数や分数になったとき、演算の意味が拡張し統合されることをより一層強調すべきである。第5・6学年での乗法・除法の意味の拡張については、現行の学習指導要領では「乗法及び除法の意味についての理解を深め」とあり、学習指導要領解説で数直線を用いた割合の意味付けが書かれている。しかし、教科書や授業では、意味の拡張を意識せず、言葉の式による指導が行われている現状がある。そこで、意味の拡張については、「乗数を割合と捉えて乗法の意味を拡張し、乗法の理解を深める」と乗法の拡張における割合の意味付けを学習指導要領に明記する。
　また、乗法・除法の意味と関わる整数倍・小数倍・分数倍の指導の位置づけや系統が明確にされていない。そのため、学力調査の結果では倍についての理解が十分とは言えない状況である。そこで、整数倍、小数倍などを何学年でどのように指導するかを明らかにすると同時に演算の意味指導を視野に入れた割合の指導系統を明確にすべきである。
　その際、演算の意味指導や計算の仕方を導き出すために有効な働きをする数直線の系統を明確にする。乗法・除法において何学年から数直線を導入し、どのように発展させるかを学習指導要領解説に明記する。

　この具体案では，割合を4年で学習するようにせよとは明記していませんが，「割合の意味の理解については学力調査などの結果から課題があることが明らかである」や「乗法・除法の意味と関わる整数倍・小数倍・分数倍の指導の位置づけや系統が明確にされていない」などから，現行どおり5年で割合を学習しているのでは良くないという問題意識を見ることもでき，これが，新しい学習指導要領にも反映されたと解釈できます。
　今後は新しい学習指導要領に基づいて，教科書が作られ*3，授業で展開することとなります。個人的には，「6mは4mの何倍か（6÷4＝1.5）」は4年の学習なのに対し，「4mの1.5倍は何mか（4×1.5＝6）」は5年となるところで，何らかの弊害が生じないか気になっています。
　なお，提言からの引用のうち，「分数の指導において，「8の1/2は4」「6の1/3は2」などの2つの数の関係を分数で表すことも扱うべきである」は，新しい学習指導要領では2年の学習となります。解説のp.106には，3行4列のアレイを用いた図が入っていました。

f:id:takehikoMultiply:20170626055710j:plain

*1:http://www.mext.go.jp/a_menu/shotou/new-cs/1387014.htm

*2:整数÷整数で基準量を求める，第3用法に相当するものも，Aの領域に入っていますが，連続量÷分離量であり，商はもとの数量よりも小さくなります。

*3:算数教科書で次に検定を受けるのは，平成31年度使用分からなので，平成32年度以降適用の次期学習指導要領との間でどうなるのかも，気にはなります。現行では，先行実施があったのですが，今回については文科省サイトでとくに公表されていません。

4a+3bの3例

　中学数学の指導する側のQ&A集です。質問部が網掛けになっているほか，図表や手書きノートが効果的に使われており，読みやすい構成となっています。
　「数と式」の問16は，「文字式の意味を具体的な事象と関連付けて読み取ることができない生徒がいます。どのように指導をすればよいですか。」とあります（p.27）。回答では，2段階の指導が提案されています。後半を書き出します（p.28）。

　文字式を提示して，それに関連する事象を考える場を設定する。例えば「4a＋3b」を提示して，この式に関連する事象を考えるようにすると，次のような場合が挙げられる。

  • 1人a円*1の品物を4つ，1つb円の品物を3つ買ったときの代金の合計
  • 時速4kmでa時間，その後，時速3kmでb時間散歩したときの距離の合計
  • 1辺a cmの正方形と1辺b cmの正三角形のまわりの長さの合計

　このような活動と共に，それを確かめる活動を通して，文字式の意味を読み取る方法が身に付くと考えられる。

　箇条書きの3つの「合計」については，小学6年の算数でも，式にすることができます（文字を用いた式）。単位は別にして，代金の合計は，a×4＋b×3と表せます。距離の合計は，4×a＋3×bです。長さの合計は，4×a＋3×bです。
　乗算記号の左が文字で右が定数，またその逆というのもありますが，これらは小学校の，「一つ分の数×いくつ分」に基づいているからです。
　その上で，中学数学の文字式のルールに従い，どの式も4a＋3bと表すことになります。
　とはいえ「文字式の意味を具体的な事象と関連付けて読み取ること」を苦手とする生徒が，4a＋3bの文字式から，この3つの例を思い浮かぶというのは，期待しにくいところです。これについて，授業でたくさん作らせるのはどうでしょうか。
　「4a＋3bで表されるような場面を書きなさい。例：お菓子a個入りの袋が4つ，同じお菓子b個入りの袋が3つあるときの，お菓子の合計」と出題します。教師は紙を用意しておき、1枚に1つの答え（場面）を書いてもらいます。苦手な生徒は1つだけでもよく，得意な生徒は何パターンも書くことになるでしょう。時間を決めて回収し，集計することで，いろいろな場面が作れることを，クラスで共有できるのではないかと思いました。

*1:原文ママ。「1つa円」と思われます。

小学校学習指導要領解説算数編（平成29年）と合わせて読みたい文献

　2017年6月21日に公開されたバージョンについて、ざっと目を通し，https://twitter.com/takehikom/status/877525224995946496から始まるツイートをしました。
　関連する文献（論文・書籍）を以下に並べておきます。

小学校学習指導要領解説 算数編

小学校学習指導要領解説 算数編

小学校学習指導要領解説 算数編

小学校学習指導要領解説 算数編

数学教育学研究ハンドブック

数学教育学研究ハンドブック

算数教育指導用語辞典

算数教育指導用語辞典

算数・数学用語辞典

算数・数学用語辞典

小学校指導法 算数 (教科指導法シリーズ)

小学校指導法 算数 (教科指導法シリーズ)

教育評価 (岩波テキストブックス)

教育評価 (岩波テキストブックス)

新版　小学校算数　板書で見る全単元・全時間の授業のすべて　2年下

新版　小学校算数　板書で見る全単元・全時間の授業のすべて　2年下

坪田耕三の算数授業のつくり方 (プレミアム講座ライブ)

坪田耕三の算数授業のつくり方 (プレミアム講座ライブ)

かけ算には順序があるのか (岩波科学ライブラリー)

かけ算には順序があるのか (岩波科学ライブラリー)

復刻版　算数・数学教育と数学的な考え方

復刻版　算数・数学教育と数学的な考え方


　本記事は，メインブログの以下の記事と連携しています。

（最終更新：2018-05-14 晩）

*1:算数（1）および算数（2）のリンクは，把握している限りでこれまで4回，URLが変更されています。ファイル名およびファイルサイズが異なっています。

学習指導要領における「順序」

おことわり：本記事の内容は，平成20年6月に公表された『小学校学習指導要領解説算数編』をもとにしています。平成29年6月21日（本記事を書いたのと同じ日）に文部科学省サイトで最初のバージョンが公開され，そのあと何度か修正がなされている，次期解説については，かけ算の「順序」について（2017.12）の後半をご覧ください。

　文部科学省が公表している，『小学校学習指導要領解説算数編』では，「一つ分の大きさ」に当たる数が乗算記号「×」の左に，「いくつ分」または「割合」に当たる数が右に出現するものを多く見かけ，その逆はありません。


　現行の学習指導要領の小学校算数は，以下で公表されています。

　乗算記号は，第2学年の用語・記号の中に，画像で表現されています。
　「×」を使った式は，例示されていませんが，それでも，かけられる数（被乗数）とかける数（乗数）の区別は，第3学年の「2位数や3位数に1位数や2位数をかける乗法の計算の仕方」や，第4学年の「乗数や除数が整数である場合の小数の乗法及び除法の計算の仕方」などから見ることができます。
　なお，乗法の交換法則が，第2学年の内容の取扱いに出現しますが，これをもとに6×4は4×6と書いてもいいと解釈するのには，無理があります。実際，その解釈に基づく教科書・学習指導案・授業例は思い浮かびませんし*1，海外でも，かけ算の交換法則を学習する授業で，先生が「2つの式が違った場面を表すのに使えないって言うの?」と生徒に尋ねる場面があります*2。
　「順序」の使われ方を，見ていくことにします。上記のページで「順序」を探すと，3か所に出現します。2つは「数の大小や順序」（第1学年，第2学年），あと1つは「起こり得る場合を順序よく整理して調べる」（第6学年）です。
　今年告示の新学習指導要領は今のところ小学校全教科で1つのPDFです。

　このPDFファイルでも，算数の節で「順序」を検索してみると，「数の大小や順序」は現行と同じです。「順序よく整理する」が第6学年に2回出現します。
　現行の『小学校学習指導要領解説算数編』（以下「解説」）も，PDFで読めます。

　「算数（1）第1章～第2章」と「算数（2）第3章～第4章」の2つのPDFファイルに分かれています。これらについての調査は，「順序」探し - わさっきにまとめてあります。
　以上より，「かけ算の順序」という意味合いの言葉は，学習指導要領および解説に出現しないと判断できます。
　もっとも近そうな記述は，第2学年の「加法，減法について成り立つ性質」のところです。解説では，「幾つかの数をまとめたり，順序を変えて計算したりする場合がある。例えば，25＋19＋1の計算を(略)16＋8の結果と8＋16の結果とを比べることで(略)」と記されています。
　これは，加法の結合法則・交換法則のことです。乗法の同様の性質は第2学年・第3学年・第4学年に出てきますが，それらの解説において，「順序」は見当たりません。
　「順序」の調査はこのくらいにして，中身を読んでいきましょう。「一つ分の数×いくつ分」に基づいた式が，解説のあちこちで出現しています。
　第2学年では「10×4は，10が4つあることから，40になると分かる」「式を読み取る指導に際しては，例えば，3×4の式から，「プリンが3個ずつ入ったパックが4パックあります。プリンは全部で幾つありますか。」というような問題をつくることができる」があります
　第3学年は，0のかけ算や，包含除と等分除のところで，「一つ分の数×いくつ分」に基づいた式が例示されています。0のかけ算について，的当ての例から，0×3と3×0とで求め方が異なっており，後者では累加が使用されていません。
　また解説の第3学年の中では，包含除と等分除，それと乗法との関連について，「包含除は3×□＝12の□を求める場合であり，等分除は，□×3＝12の□を求める場合である」と示しています。これも，「一つ分の数×いくつ分」が背景にあります。
　ところで，この関連を示した段落では「包含除も等分除と同じ仕方で分けることができる*3ことなどにも着目できるようにしていくことが大切である。そのようにして，どちらも同じ式で表すことができることが分かるようにする」とも書かれています。
　ここで「包含除や等分除なんて区別を考える必要ないじゃないか」と考えてみるのはどうでしょうか。実際その方針をとっているブログもあります。
　とはいえその区別は，算数教育で当然のものとなっています。国内に限った話ではなく，米国各州共通基礎スタンダード(Common Core State Standards)のMathematicsについて，かけ算・わり算の関係が，表になっています。

　パターンは「a x b = ?」「a x ? = p and p ÷ a = ?」「? x b = p, and p ÷ b = ?」の3種類です。
　ただし米国ということもあり，「いくつ分×一つ分の大きさ」で解釈します。「a x ? = p and p ÷ a = ?」は一つ分の大きさを求めるほうなので等分除，「? x b = p, and p ÷ b = ?」はいくつ分を求めるので包含除に，対応づけられます。
　もう少し古いものだと，Greerの分類表が知られています（かけ算・わり算でモデル化される場面 - わさっき）。
　包含除や等分除の区別に関しては，「除法が用いられる場面」として，その2種類が代表的なものだ，と言って差し支えないでしょう。そして教科書や学校の指導では，配る操作を通して，場面に合う分け方ができ，わり算の式や，かけ算との関連，また配らないわり算（6mは3mの何倍かなど）への適用と，展開していきます。
　啓林館と教育出版の3年上の教科書を見ると，数図ブロックを用いた2種類の分け方が図になっています。啓林館は等分除が先で，教育出版は包含除が先です。1つのわり算の式から，包含除・等分除の場面が作れることは，どちらの教科書にも載っています。
　「かけ算の順序」と包含除・等分除の件で，分量をとりすぎてしまいました。上の学年を見ていきます。wikipedia:かけ算の順序問題の改訂にあたり，解説より抜き出して記載したのは，以下のとおりです。

高学年では小数の乗法を学習するが，第4学年では乗数が整数である場合に限られる。0.1 × 3ならば，0.1 + 0.1 + 0.1の意味である。

第5学年では乗数が小数となる乗法を学習し，「1mの長さが80円の布を2.5m買ったときの代金」は，80 × 2.5で表される。言葉の式についても，「1mの重さ × 棒の長さ = 棒の重さ」「（単価）×（個数）=（代金）」と一貫している。

なお中学校学習指導要領解説数学編では，いくつかの言葉の式と並んで「（値段）=（単価）×（個数）」が記されている。

　上記は「×」を用いた数の式または言葉の式の例ですが，「×」がなくても，被乗数と乗数の意味の違いが考慮されています。現行では，「小数×整数」のタイプのかけ算を第4学年で，「整数×小数」「小数×小数」を第5学年で学習します（その際，かける数は「いくつ分」という分離量から，「割合」という連続量に拡張されます）。分数についても，「分数×整数」は第5学年，「分数×分数」は第6学年です*4。


　今年告示の学習指導要領について，解説はまだ出ていませんが，各学年の「数と計算」の学習内容には現行と大きな差がないことから，変更されないと思われます。昨年，日本学術会議の数学教育分科会が出した提言については，メインブログのhttp://d.hatena.ne.jp/takehikom/20161122/1479743916で紹介しています。
　最後に，現行の解説には，「例えば「ひもを4等分した一つ分を測ったら9cmあった。はじめのひもの長さは何cmか。」のような場合にも，乗法が用いられることを理解できるようにする」も収録されています*5。第3学年です。具体的に紐を用意するのでも，この場面を図示するのでもいいのですが，これについては一つ分の大きさが9cmで，4つあるので，式は9×4＝36が期待されます。「6人に4個ずつミカンを配ると，ミカンは何個必要ですか」（『かけ算には順序があるのか (岩波科学ライブラリー)』まえがきより）と同様に，出現する2つの数をひっくり返して，かけ算の式にすることが想定されており，算数の3年の教科書や問題集にも，この種の文章題が見られるのは，留意しておきたいところです。

*1:6行4列のアレイに対して，6×4と4×6の式を立てることは可能です。その場合にも，交換法則を根拠としているのではなく，それぞれのかけ算の式は，「一つ分の数×いくつ分」に基づいています。

*2:http://d.hatena.ne.jp/takehikom/20150822/1440184614

*3:個人的にはこの記述に違和感があります。第1学年の「具体物をまとめて数えたり等分したりし，それを整理して表す活動」が関連し，解説では「具体物を等分することについては，全体を同じ数ずつ幾つかに分けたり，全体を幾つかに同じ数ずつ分けたりする活動を扱う。例えば，8本の鉛筆を，2本ずつや4本ずつなど，同じ数ずつ分けると何人に分けられるかを操作や図で説明したり，分けられた結果を式に整理して表したりする」と具体化されているのですが，それらから，「包含除も等分除と同じ仕方で分けることができる」の素地となるものを見出せないのです。「等分除も包含除と同じ…」であれば，累減を用いて操作（そして説明）ができます。なお，トランプ配りに限らない，子どもたちの配り方については，http://ci.nii.ac.jp/naid/110001898376よりダウンロードできる論文で詳しく書かれています。

*4:新しい学習指導要領では，「乗数や除数が整数や分数である場合も含めて，分数の乗法及び除法の意味について理解すること。」の記載により，「分数×整数」も第6学年での学習となります。

*5:文部省が「小学校指導書」として公開してきたものにも，見られます。http://d.hatena.ne.jp/takehikom/20140131/1391118525

「割合」とその周辺

　#掛算や#超算数では，ときどき「割合」関連のツイートを見かけます。
　ツイートを離れ，小学校算数の「割合」とその周辺の情報を，自分なりに整理することにしました。
　はじめに，簡単にまとめておきます。

  • 割合の文章題の例は，『小学校学習指導要領解説算数編』より読むことができます。
  • 割合である場合，そうでない場合を含め，「小数の乗法及び除法」を5年で学習します。
  • 式のパターンは「B×P＝A」「P＝A÷B」「B＝A÷P」の3種類です。割合の三用法と呼ばれます。
  • 割合の文章題を解くツールには，「みはじ」「2重数直線」などがあります。
  • 今年3月に告示された学習指導要領によると，速さは5年で学習することになります。

　以下，誤解されない場合には「第x学年」を「x年」と表記しています。

文章題に見る，割合

　割合の文章題の例は，『小学校学習指導要領解説算数編』に載っています（PDF版ではpp.166-167）。5年です。
　「1メートルの長さが80円の布を2.5メートル買ったときの代金が何円になるか」については，80×2.5という式で表せることを述べてから，B×P＝Aという文字式を示しています。
　ここでBは「基準にする大きさ」，Pは「割合」，Aは「割合に当たる大きさ」です。2.5メートルが割合というのは，ちょっと分かりにくいところですが，80×2.5の式の直前に「布の長さが2.5倍になっているので，代金も2.5倍になるということから」と書かれており，これが理由となります。
　わり算は2種類あります。P＝A÷Bと表す場合，AはBの何倍かを求めることとなり，包含除の考えに対応します。文章題は「9メートルの赤いリボンは，1.8メートルの青いリボンの何倍になるか」で，式は9÷1.8です。
　B＝A÷Pで表されるわり算も，あります。基準にする大きさを求めるもので，等分除の考えに対応します。文章題は「2.5メートルで200円の布は，1メートルではいくらになるか」で，式は200÷2.5です。
　3つの文字の意図は書かれていませんが，Bはbase，Pはproportion，Aはamountの頭文字と考えることができます。Bについては「基準量」「土台量」，Aは「比較量」「比べる量」「比べられる量」と書かれることもあります。上記の2.5メートルのように，割合が，いわゆる無次元量ではなく具体的に測定できるものであれば，「測定値」という表記も知られています。昭和43年（1968年）告示の学習指導要領には「ＡのＢに対する割合（Ｂを単位としてＡを測った値）がｐであるとき，Ａを，Ｂ×ｐとして求める」が入っています。
　「1より小さい数をかけると，積は，かけられる数よりも小さくなる」や「1より小さい数でわると，商は，わられる数よりも大きくなる」も，この段階で学習します。

小数のかけ算・わり算

　ここまでについて，「割合」の用語が使われているものの，『小学校学習指導要領解説算数編』の該当箇所では，これを割合の理解や学習とみなしていません。かわりに「乗数や除数が小数である場合の乗法及び除法の意味について理解すること」と書かれています。
　上で理由を書いたものの，2.5メートルを割合に対応づけるのは，直感的ではありません。これについては2重数直線を使用し，かけ算の件であれば「1メートル」「80円」「2.5メートル」「□円」を数直線上に配置して，1メートルと2.5メートルから「2.5倍」を得る流れが期待されます。
　「小数の乗法及び除法」を，割合と直結させていないのはなぜかですが，面積計算を含む，他の種類のかけ算・わり算への適用を考慮しているため，と考えることもできます。
　例えば，長方形の面積を求める問題について，「たて8cm，よこ2cm」と「たて8cm，よこ2.5cm」と「たて8.3cm，よこ2.5cm」とで，扱いが異なってきます。最初の例は，1cm×1cmの単位正方形が8×2個（または2×8個）と考えることで，4年でも計算できます。2番目の例は，「たて×よこ＝面積」の公式に当てはめるなら，8×2.5ですが，「よこ×たて」に当てはめるなら2.5×8で，そうすれば，4年の範囲内で計算できます。3番目の例は5年（小数の乗法）であり，積に，100分の1の位の数が出現することにも，注意しないといけません。
　ところで，小学校の算数で「小数の乗法」といえば，かけられる数が小数の場合であり，5年で学習します。かけられる数が小数で，かける数が整数の場合の乗法は，4年の学習事項です。0.1×3＝0.1＋0.1＋0.1のように，累加で求められます。小数の乗法では累加で求められず，意味の拡張が必要となる，というのが，1960年代の中島健三による著作より知ることができ，現在の学習指導要領でも同じ立場となっています。
　それから，「円周率」も割合です。「円周の直径に対する割合のことを円周率という」は，『小学校学習指導要領解説算数編』でも記載されています。円周率の学習（どんな大きさの円についても，円周の直径に対する割合が一定であることも）とともに，直径の長さから演習の長さやその逆を計算で求めることを，5年で学びます。円の面積は，6年です。
　解説のつかない，「小学校学習指導要領」の5年で言及されている「割合」は，「異種の二つの量の割合」です。人口密度（混み具合）が，解説で例示されています。「単位量当たりの大きさ」とも書かれます。

割合の三用法

　割合のかけ算・わり算について，式のパターンは「B×P＝A」「P＝A÷B」「B＝A÷P」の3種類です。「P×B＝A」は学習しません。
　3種類あることについて，古くは「比の三用法」，そして現在では「割合の三用法」と書かれます。その場合，割合を求める式の「P＝A÷B」が第一用法となります。かけ算の「B×P＝A」が第二用法，もう一つのわり算の「B＝A÷P」が，第三用法となります。
　1つのかけ算・2つのわり算で対応づけられることについては，国内に限った話ではなく，Greerの分類表や，米国Core Standardの表などからも，知ることができます。
　小学校3年のかけ算・わり算文章題を対象とした作問学習支援システムが，2017年1月1日付けで，ある論文誌に掲載されています。「割合の三用法」に基づいていることが，本文で記されています。

割合理解の支援

　割合の文章題に対して，適切な式を立てること（演算決定）を支援するためのツールも，いくつか知られています。
　速さに関しては，「みはじ」などと呼ばれる図があります。道のりの「み」，速さの「は」，時間の「じ」を以下のように配置します。

　3つのうち，未知のものを隠せば，わり算またはかけ算で，その未知の値を計算できる，というわけです。
　この種の図は中学1年の教科書（ただし，小学校の学習内容の復習として）や，海外の学術書，また子ども向けの本でも見かけます*1。割合では「くもわ」または「く・わ・もと」に置き換えられます。
　小学校の算数で，「みはじ」または同種のツールがどのくらい，活用されているかは不明ですが，ある学力調査の応用問題は，示唆を与えてくれます。東京都算数教育研究会が実施しているもので，次の出題です。

　2つの小問のうち，「道のりのちがいは，何kmになりますか。」と問う(2)は，「みはじ」だけでは困難と言っていいでしょう。
　東京都の児童，約60,000人が解答していて，(1)の正答率は90%ほど，(2)は70%台後半です。他の問題の正答率と比較しても，(2)の出来が良いと言えます。推測ですが，(2)の類題が教科書にあるのではないか---結局のところ，速さといえば「みはじ」ではない，と思われます。
　また別のツールも知られています。2本の数直線を上下に並べ，0を左端とし，右に伸ばします。2つの数直線（異なる量）の間で，「1メートルの長さが80円」のような，対応づけされる値は，上下で同じ位置にします。
　単純な数直線と区別するため，「比例数直線」または「二重数直線」と書かれることがあります。米国Core Standardでは，"double number line diagrams"という用語を見かけます。『小学校学習指導要領解説算数編』には，1とBとPとB×Pを含む数直線の図が掲載されていますが，この種の数直線が算数教育で活用されるきっかけとなった，白井らの論文では，以下のように，既知の値と未知の□とで表現しています。
f:id:takehikoMultiply:20170614062311j:plain
　ただしこの図式表現に関連するものは古くからあり，例えば横線は1本で，上下に異なる（対応する）量の値を書くものや，「∠」の形のように，ゼロを1点にして2方向に伸ばすものもあります。また数直線にしなくても，2×2や，列の数を増やした表も，実質的には同じものと言えます。ただし数直線にすると，大小関係（「1より小さい数をかけると，積は，かけられる数よりも小さくなる」なども）が視覚化でき，倍操作（ある値からある値に矢印を向けて「2.5倍」などと書くことがあります）が形式的にならない，というメリットもあります。

どんなことを何年で学ぶか

　現行の学習指導要領などは，平成20年（2008年）告示されたものです。そこでは，「割合」の用語は5年に出現します。
　かけ算に関して，小数×整数は4年，整数または小数×小数は5年，分数×整数は5年，分数×分数は6年で学習します。わり算も同様ですが，20÷8＝2.5（2あまり4ではなく）と計算する「割り進み」も，4年に含まれています。
　比例の用語も，5年で学習します。比例の詳しい学習や，問題解決などは6年です。比の概念も6年です。円周率の学習と直径・半径・円周の計算などは5年，円の面積は6年です。
　今年（平成29年，2017年）告示の学習指導要領では，割合や，小数のかけ算・わり算は5年で学習しますが，いくつか違いもあります。
　かけ算に関して，分数×整数は，6年に移っています。分数÷整数も同じです*2。一方，速さは，5年に変わります。「異種の二つの量の割合」「単位量当たりの大きさ」として，取り上げられています。
　新しい学習指導要領では，ABCDの領域に変更がありました。「A 数と計算」はそのままですが，「B 図形」（これまではC），「C 測定」は3年までで4年からは「C 変化と関係」，そして「D データの活用」が新設されています*3。
　「割合」は，5年の目標に「整数の性質，分数の意味，小数と分数の計算の意味，面積の公式，図形の意味と性質，図形の体積，速さ，割合，帯グラフなどについて理解するとともに(以下略)」と明記されました。
　なのですが，4年に「割合」の用語が出現します。Cの領域で，「簡単な場合について，ある二つの数量の関係と別の二つの数量の関係とを比べる場合に割合を用いる場合があることを知ること。」と書かれています。
　割合の導入としてこれまで用いられている，バスケットボールなどのシュートのうまさが，これからの教科書では4年に掲載される，という可能性が考えられます。
　新しい学習指導要領に基づく「解説」は，まだ出されていません。個人的には，昨年，日本学術会議数理科学委員会数学教育分科会が出した「初等中等教育における算数・数学教育の改善についての提言」の脚注に見られる二次元表が，小学校の算数の解説に入るのか同か，そして表から割合を求めるような学習が，教科書に載るのか，教科書外の学習事例として展開されるのかが，気になっています。

関連情報

*1:ただし「速さ」など，異種の二つの量の割合は，左下に置かれ，かけ算の式では，かけられる数になります。この量を一定としたとき，道のりは時間に比例します。速さや単価といった「1あたり量」は，比例定数となり，y＝axのaに対応づけられます。

*2:「乗数や除数が整数や分数である場合も含めて，分数の乗法及び除法の意味について理解すること。」が，第6学年 A（数と計算）に記載されています。

*3:これまでの「D 数量関係」の内容は，AまたはCの領域に移行し，学習事項で削られたものは見当たりません。例えば四則の混合した式などは，現行では4年D，新しいものでは4年Aです。比例については，現行では5年Dと6年D，新しいものでは5年Cと6年Cです。