コメント経由で:
じゃ、どちらの順序でも書けて、かつ説明を要する問題はどんなか、と言えば、例えばこんなの。
例題2.5人の子供に1個ずつ飴を配りました。1回配ったらまだ飴があったので、また1個ずつ配りました。これを4回配ったところで飴が終わりました。配った飴は全部で何個でしょう。
これに対する回答は、掛算の順序に拘っても、次の二つが考えられる。
回答2?.1人につき4個の飴が配られたので、掛けられる数は4。子供は5人いるので、掛ける数は5。式:4×5=20 答:20個
回答2?.1回で5人に1個ずつ、つまり5個の飴を配ったので、掛けられる数は5。全部で4回配ったので、掛ける数は4。式:5×4=20 答:20個
この流れを読んで,思い浮かんだ本が2冊あります.

- 作者: 関西算数授業研究会
- 出版社/メーカー: 東洋館出版社
- 発売日: 2014/08/29
- メディア: 単行本
- この商品を含むブログ (4件) を見る

- 作者: 齋藤昇,小原豊
- 出版社/メーカー: 東洋館出版社
- 発売日: 2013/09/21
- メディア: 単行本
- この商品を含むブログ (13件) を見る
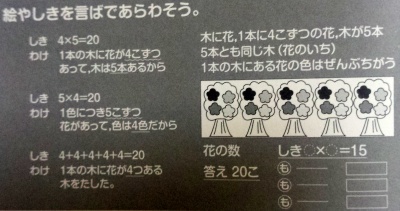
かけ算の授業例は,p.23から始まります.「とらえ方によってはどちらも1つ分の数として見ることができる絵」を使っています.問題ほかは,撮影したものを(p.24):
算数の教え方,数学的に考える力 - わさっき
授業の流れを見ていくと,ある児童が「5×4=20 答え20個です」と言ったのに対し,すぐに別の児童が「逆だよ」と言い,先生の介入もあって結局,「赤い花が5こ,青い花も5個,紫の花も5個,黄色い花も5個で,どの花も5個ずつで,花の色は4色あるからだよ」という言葉により,5×4も正しい式としています.
2013年はトランプ配り,1988年はアレイ - わさっき第2に,既習内容や発展内容に高い見通しをもつことで,子どもの問題解決上の気づきをより的確に評価できることです。例えば,「3人の友だちにみかんを4こずつあげます。みかんは全部でいくついりますか」という問題に対して,田中さんは3×4=12,鈴木さんは4×3=12と立式して答えを求めたとします。これを“みかん4こが3人分必要”だから,田中さんは誤っていると評価することも,3×4=4×3だからどちらも正しいと演算の交換法則を式解釈に持ち込んで評価することも早計といえます。
算数・数学の問題解決を乗法構造という立場から特徴づけて捉えるベルニョの見解によれば,鈴木さんの立式からは,友達1人と3人の間と,みかん4こと□この間に同じ関係を認めており,いわゆる倍操作を行っています。これに対して,田中さんの立式からは,友達1人とみかん4この間,友達3人とみかん□この間に同じ関係を認めており,いわゆる関数的な操作を行っています。もし田中さんが「3人の友達にみかんを1つずつあげれば,みかんは3ついる。これを4回繰り返せばいい」と関数的に考えていた場合,式は3×4となり,正しい立式として評価することができます。
ということで,5ドルのおもちゃの車が4個なら,総額を表す式は4×5でも5×4でもいいんだ,「3人の友だちにみかんを4こずつあげます」[齋藤2013, p.9]も,4×3でも3×4でもいいんだ,かけ算の順序問題は「どっちでもいい」で解決だ…
かけ算と構造 - わさっき
というのがどうやら期待されていない記述が,[Vergnaud 1988, p.146]に見られます.(略)
そういったわけで,「3人の友だちにみかんを4こずつあげます」について3×4を正解とするのは,2年生の段階よりも,高学年でその意義を見出したいところです.2年生の授業では,3×4と書いたら,3+3+3+3という式とともに,「12人になっちゃう」「みかんを3こずつ4人にあげることになっちゃう」といった解釈とともに,その式が場面に合わないことを確認するのは,「かけられる数」「かける数」そして数量関係の理解としてちょうど良いと言えます.これは,上記のa-dのうち,「c」よりも「a,b,dの組み合わせ」を重視しよう,ということでもあります.
冒頭の「例題2」について,そういった出題が算数の授業でなされ,かけられる数とかける数を交換した2つの式を正解(その場面を表す式)とすることには,どちらかというと賛成*1なのですが,算数において考慮済みあるいは類例ありの話について,批判的な情報発信をしている人々が整理しようとしない状況を,残念にも思います.
別トピックの「類例」を一つ.
掛算を最初に教えるとき、その順序に拘るのなら、順序が一意に決まるような問題文は駄問だね。どちらの順序でも正解になりうるようにして、なおかつ、なぜその順序にしたのかを説明させないと、児童が本当に理解したかどうかを判断することはできない。
思い浮かぶのは:
「子どもが7人います。1人に4個ずつアメをくばります。アメはみんなで何こいりますか」という問題に対して、7×4=28答え28こ、と解答した小学校2年生の子がいました。この解答をどのように解釈して、どのような対応をしたらよいか、乗法の意味と関連させてまとめてみましょう。
(『小学校指導法 算数 (教科指導法シリーズ)』p.96)
小学校教師を目指す学部生向けの本と思われます.解答は載っていません.本文からすると,4×7=28で表すよう指導することが,意図されていますが,この設問に限って言うと,本人が7×4でいいのだとする理由を的確に説明できれば,正解にしてよい,という余地もあります.
*1:ただし,「配る」操作への配慮も必要です.トランプ配りが乗法ではなく等分除の素地となっていることは,http://d.hatena.ne.jp/takehikom/20130605/1370382764に載せた文献から確認できます.