小学校算数のかけ算の話でアレイは,大人にとっても難しい,または混乱を招きやすいのかもしれません。再調査してみました。
1. 素朴なアレイ図と加工されたアレイ図
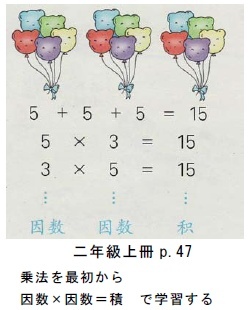
はじめに,「アレイ図」の例を4つ,示します。
それぞれの図の出典です。
- [6 by 9アレイ]と,{a,b,c}×{x,y}の図は,「乗法の意味についての論争と問題点についての考察」https://doi.org/10.32296/jjsmep.50.6_74
- □と△と○が3つの絵は,『誰もができる子どもに活用力をつけるワクワク授業づくり―第2回RISE授業実践セミナーの報告』p.69(場面を表すかけ算の式は,1つか,2つか)
- 丸うが正解の問題は,東京都算数教育研究会の令和3年度実態調査 第2学年 大問5(1) https://tosanken.main.jp/data/jittaityousa-kousatu/R04jittaityousakousatsuad/%E7%AC%AC%EF%BC%92%E5%AD%A6%E5%B9%B4%E7%B5%90%E6%9E%9C%E3%81%A8%E8%80%83%E5%AF%9F.pdf#page=3
実態調査の件は,同じページの解説文に「問題場面の数量関係に着目し,乗法の意味に基づいて被乗数と乗数を捉えてアレイ図に表し,立式することができるかをみる問題である。」と書かれています。
とはいえ「アレイ図に表し」ているのではなく「もんだいに 合う 図を えら」ぶ問題ですし,丸あ・丸い・丸のように,1つ分の数といくつ分が読み取れる状態の絵を「アレイ図」と呼ぶのには,戸惑いを覚えます。
4つの図を比較すると,[6 by 9アレイ]が,「素朴なアレイ図」であり,他の3つは,それぞれ異なる方法で「加工されたアレイ図」と見なすことができます。
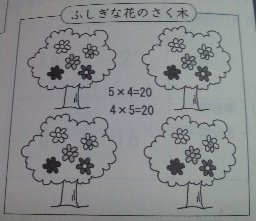
「素朴なアレイ図」に書き足したり,記号を変えたりして,「加工されたアレイ図」を構成するのが自然な流れ,と言いたいのですが反対の事例もあります。『小学校学習指導要領(平成29年告示)解説算数編』p.128の「縦に3段あること,横に4列あることが見いだせれば,3×4,又は4×3と式で表すことができる。」の件です。
写真をよく見ると,掲示物は列ごとにつながっています(最上段の上と最下段の下にはないので,つなぎではなく氏名や作品タイトルを書いたものだ,というのは無理があります)。このつながりも考慮に入れれば,写真を表すかけ算の式は,3×4のみである,という見方ができます。
しかし解説によると,この場面に対する式は「3×4」「4×3」の2つです。合計8個のつなぎを取り除くことが,「加工されたアレイ図」を「素朴なアレイ図」に変換する行為となっています。
2. アレイと,直積と,その中間
小学校算数のかけ算において,「アレイ」と「直積」を区別するのが有用に思えてきました。「同数グループ」と合わせて,それぞれの特徴は次のように表せます。
- アレイは同数グループに帰着して,式に表したり総数を求めたりできる。
- 直積はアレイに帰着して,総数を求めることができる。
- 直積は(アレイを経ずに)同数グループに帰着して,式に表したり総数を求めたりできる。
- アレイの各要素はそれぞれ区別されない。
- 直積の各要素はそれぞれ区別される。
- 同数グループの各要素は(ヒトやモノなど物理的には異なるかもしれないが,かけ算の式に表して求める際には)区別されない。
Greerによる分類表(サンドイッチの乗法構造)と照合すると,「同数グループ」は,Equal groupsのことです。「直積」は,Cartesian product(デカルト積)に対応づけるのがよさそうです。「アレイ」に一対一に対応するものはなく,Cartesian productに含まれるものと見なされます。また「帰着」の語は,前掲の「乗法の意味についての論争と問題点についての考察」(https://doi.org/10.32296/jjsmep.50.6_74)の本文に出現します*1。
さらに事例をみていくことで,「アレイの各要素はそれぞれ区別されない。」とも「直積の各要素はそれぞれ区別される。」とも異なるタイプの図があることに気づきました。「各要素の間で,同一のものがある。」と表すことができます。当ブログとメインブログから,いくつか挙げます。
ではその順序とやらに基づきこれを解いてもらえますかね? pic.twitter.com/QBWye23dqS
— 数学の人 (@regulus_math) February 16, 2024
3×2と2×3のどちらでも求めることができる場面について,次のように形式化できます。
- 直積は,例えば{a,b,c}×{x,y}です。これは{x,y}×{a,b,c}と,集合としては異なりますが,要素数は同じです。
- 「各要素の間で,同一のものがある。」は,多重集合を使用して,例えば{{a,b,c},{a,b,c}}です。これは{{a,a},{b,b},{c,c}}と,多重集合としては異なりますが,要素数は同じです。
なぜ3×2と2×3(または,a×bとb×a)のどちらでも求めることができるかというと,この場面も,同数グループに帰着できるからです。その際,「1つ分の数(かけられる数)」は2種類あります*2。図からも,集合・多重集合からも,2種類の「1つ分」を見つけることができ,選んだ「1つ分」に基づき「いくつ分」が決まるのです。