かけ算の順序の昔話

算数教育について気楽に書いていきます。

場面を表すかけ算の式は，1つか，2つか

　学習指導要領とその解説，教科書・学習指導案・授業事例を総合すると，かけ算の式について，（国内の小学校の）算数の2～3年で学ぶのは，以下のとおりとなります。

  • かけ算の式を，言葉を使って表すと，「1つ分の数×いくつ分＝ぜんぶの数」です。
  • 倍の場面では，そこから1つ分の数といくつ分を特定し，かけ算の式に表したり，その逆を行います。
  • 倍の場面では，かけられる数とかける数を反対にした2つの式（2×3と3×2など）が，異なる場面を表すことも学びます。
  • 積の場面では，そこから1つ分の数といくつ分のペアを自分で決めて，かけ算の式に表したり，他の児童が表したかけ算の式の読み取りを行います。

　いくつか補足します．まず，箇条書きより前の「かけ算の式」は，小学校学習指導要領の算数*1に記された「乗法が用いられる場面を式に表したり，式を読み取ったりすること。」を，簡潔に表したものです。次に，言葉の式はよく「1つ分×いくつ分」と略記されますが，これでは被乗数と乗数の非対称性---この語はあとの引用で出現します---やそれぞれの役割が見えにくくなるため，推奨しません。「それぞれの役割」を具体的に挙げると，積は被乗数と同種の数量となること，そして乗数は（問題文では「5皿」「2.3m」のように具体的な数量で表されるとしても，かけ算の式においては）「何倍か」を意味することなどです。
　「倍の場面」*2というのは，Greer (1992)の分類*3を用いるならEqual groups*4，「積の場面」はCartesian productです。そして「積の場面」であっても，「倍」の考え方に基づいて立式する*5ので，1つ分といくつ分のペアが複数，見つけられることになります。
　「2つの場面がそれぞれa×bとb×aで表される」と「1つの場面を表す式としてa×bもb×aも認められる」は共存します。後者の例（アレイや直積に基づくもの）を示したところで，前者は駆逐されない，と言うこともできます。


　メインブログ・当ブログから，事例を紹介します。

　この次のツイートで，『小学校学習指導要領（平成29年告示）解説算数編』p.128の記述をいくつか抜き出しました．実際の文章は次の通りです（全角数字は半角に換えています）．

　例えば，映像を見て，そこに表されたものの数をブロックで並べる活動を行う。左のような映像を見て全部で幾つあるかを考える際，「同じ数ずつ」あることに気付くことができれば，それが幾つあるのか，まとまりの個数を数える必要性が生まれる。串が3本あること，団子が4個ずつ並んでいることを見いだせば，同じようにブロックを並べることができる。全部の数も，並べた後で数えることができる。
　この団子の数は，数えると12個である。式で表現すれば，4＋4＋4と表現できる。しかし，その式では3本と見いだした数を直接表現できていない。そのことを表すために乗法を使って4×3という式に表すことを知る。
　また，右のような場面では，「同じ数ずつ」縦横に並んでいることが共有できれば，何をみればよいかが焦点化できる。「縦は何段か。」「横は何列あったか。」などである。それらが分かれば，ブロックを並べることができる。縦に3段あること，横に4列あることが見いだせれば，3×4，又は4×3と式で表すことができる。答えは，3＋3＋3＋3として求めることもできるし，並べたブロックを数えて求めることもできる。

　このうち串に刺した団子の総数を求めるのは「2つの場面がそれぞれa×bとb×aで表される」に該当し，「また，右のような場面」から始まる，4行3列の掲示物は，「1つの場面を表す式としてa×bもb×aも認められる」になります．
　プログラミングで「1つの場面を表す式として2×5も5×2も認められる」ものは，上に示した通りです．「2つの場面がそれぞれ2×5と5×2で表される」ようなシチュエーションは，写経型学習をもとに例示できます．プログラムを「毎日2つずつ，5日間写経する」のと，「5つずつ，2日間写経する」のとで，写経の総数は同じですが，1つ分の数といくつ分が違っています．

　上の引用に2つ，補足します。「この次のツイート」は，https://twitter.com/takehikom/status/1447685396779835401から始まるのですが現在リンク切れです。『小学校学習指導要領（平成29年告示）解説算数編』p.128は，https://www.mext.go.jp/content/20211102-mxt_kyoiku02-100002607_04.pdf#page=134で見ることができます。

(p.276)
A situation in which there is a number of groups of objects having the same number in each group normally constitutes a child's earliest encounter with an application for multiplication. For example,

3 children have 4 cookies each. How many cookies do they have altogether?

Within this conceptualization, the two numbers play clearly different roles. The number of children is the multiplier that operates on the number of cookies, the multiplicand, to produce the answer. A consequence of this asymmetry is that two types of division may be distinguished.
（いくつかのグループがあって，各グループで同じ個数のモノがあるときというのが，通常，子どもが最初にかけ算を適用する場面となります。例えば

3人の子どもが4枚ずつクッキーを持っています。全部合わせるとクッキーは何枚ですか。

　これをかけ算の式で表そうとするとき，2つの数は明らかに異なる役割を担います。子どもの数は「乗数」であり，クッキーの数すなわち「被乗数」に作用して，答えとなる総数が得られます。この非対称性の結果として，2種類のわり算が区別されます。）

(p.277)
Cartesian products provide a quite different context for multiplication of natural numbers. An example of such a problem is

If 4 boys and 3 girls are dancing, how many different partnerships are possible?

This class of situations corresponds to the formal definition of m × n in terms of the number of distinct ordered pairs that can be formed when the first member of each pair belongs to a set with m elements and the second to a set with n elements. This sophisticated way of defining multiplication of integers was formalized relatively recently in historical terms.
There is a symmetry between the roles of the two numbers here, and hence only one type of division problem. Given that there are 12 possible partnerships, there is no essential difference between (a) being told that there are 4 boys and asked how many girls there are and (b) being told that there are 3 girls and asked how many boys. (In fact, it would be unusual to pose division problems of this type.)
（デカルト積は，自然数の乗法に対してまったく異なる文脈を提供します。そのような問題の例は

4人の男の子と3人の女の子がダンスをしているとき，男女のペアは何通りできますか。

　このような状況は，m×nを，各ペアの最初のメンバーがm個の要素を持つ集合に属し，2番目のメンバーがn個の要素を持つ集合に属するときに形成できる，異なる順序のペアの数によって，形式的に定義することに対応します。このように整数の乗算を定義する洗練された方法は，歴史的に見ると比較的最近になって公式化されたものです。
　この場合，×の前後に書く2つの数の役割は対称性を持ち，したがって除法の問題は1種類だけとなります．男女のペアは12通りであることを前提として，「(a) 4人の男の子がいるとき，女の子は何人いますか」と「(b) 3人の女の子がいるとき，男の子は何人いますか」の間に本質的な違いはありません。（むしろ、この種の除法の問題を出す方が珍しいのですが。））

　タイトルを日本語に訳すと「かけ算に関する教科書の分析—日本，シンガポール，タイの事例」といったところでしょうか。著者はともにタイの研究者です。TIMSS（国際数学・理科教育調査）で日本とシンガポールは非常に良い成績をあげており，その理由を，タイを入れた3か国の教科書に求めようという内容です。
(略)
　[Boonlerts 2013]は，また別の情報源と照合することもできます。本文で「Greer (1992)」と書き，引用している文献です。かけ算の学習におけるtypes of multiplication（乗法が用いられる場合）として，日本の教科書は「equal group（同等のグループ）」「rectangular array（2次元アレイ）」「multiplicative comparison（乗法的な比較）」の3つが使用されているのに対し，シンガポールは「同等のグループ」「2次元アレイ」の2つ，そしてタイは「同等のグループ」のみだというのです。

　教育出版・東京書籍・啓林館の算数教科書で，イラストではなく写真をもとに，かけ算の式で表すことが期待されているページがありました。
　教育出版『小学算数』2下ではp.9です。「みのまわりから，かけ算の式であらわせるものを見つけましょう。」の下に，4つの写真があります。傘立てについては，「かさ立てのあなの数は，4こずつ9れつ分です。」という文と，「4×9＝36」の式も，書かれていましたが，他は写真のみです。くつ入れは，4つずつの6段と見れば，4×6の式が思いつきますが，ここは6×4でも良さそうに見えました。
　東京書籍『新しい算数』2下はp.12です。「学校の 中で かけ算の しきに 書ける ばめんを さがしましょう。」となっていて，写真は，「つくえ」「お面」「掲示物」「ロッカー」です。ぱっとみて思い浮かぶ式は，順に，「2×6」「5×8」「5×3」「3×7と7×3」です。
　啓林館『わくわく算数』2下だとp.9です。「みの まわりから，かけ算の しきで かける ものを みつけましょう。」の文と，写真は4つです。木のキューブを1個ずつ，少しだけずらして3段に積み重ねたものが，最初に目を引きました。面の数を求めるなら，6×3＝18で18面となります。他には，4枚の花びらの花が3つ，5個を刺した串団子が3本。キューブもそうですが，式はありません。ロッカーの写真には，「たてに6この8つ分だから，6×8＝48になります。」が添えられていました。

　「かけ算の順序」に関連する記述が見られるのは，特色2です。「3年上p.2～3」すなわち3年の最初の問題は，●の個数を工夫して求めるものですが，しほさんは5×4＝20，こうたさんは4×5＝20の式で表し，答えはともに「20こ」です。「しほさんやこうたさんの考えをせつ明しましょう。」に関して，すぐ上の吹き出しや，2年で学習した内容をもとに，「しほさんは，5このまとまりが4つ分とみて，5×4＝20という式にしました」「こうたさんは，4このまとまりが5つ分とみて，4×5＝20というしきにしました」と答えることが期待されます。この件において，かけられる数とかける数を交換した式が認められるのは，意図したものでしょう。

　上記の「特色2」につけたリンク（https://ten.tokyo-shoseki.co.jp/text/shou/sansu/introduction/page02.html）は現在，適切な情報が取得できず，Wayback MachineでURLを指定してもうまくいきません。

　「意味」の語が見当たらないものの，「かけ算の意味」と「かけ算の式の意味」の違いに注意した，学習指導案のPDFファイルが，以下よりアクセスできます。

　終盤に，「かけ算が使えるようにする考え方をルーブリックにより評価する。」を2重線で囲んで，1つの文章題を提示し，子どもの自由な表現を引き出す試みを行っています。文章題は以下のとおりです。

２年生は「みどり組」「白組」「赤組」の３クラスあります。
では，ふぞく小学校ぜんぶでは，何クラスあるでしょう。なるべくかんたんにもとめる
方ほうを考えて，図やしきやことばをつかってせつめいしましょう。
（ヒント　１年生は「月」「空」「にじ」「ほし」の４クラスあるよ）

　注意したいことが1つあります。3×6＋1＝19も6×3＋1＝19も，正解となっています。というのもこの学校では，1階・2階・3階に6クラスずつ，そして4階に4年緑組があるからです。

　今年出版のまた別の本では，「一つの場面に対して，かけられる数とかける数を交換した2つのかけ算の式で表せること」が特徴的でした。

　「かけられる数とかける数を交換した2つのかけ算の式で表せる」について，どのような場面でも交換できることは意図されていませんし，交換可能な場面はいずれも，図として提示されています。「さらが 5まい あります。1さらに りんごが 3こずつ のって います。りんごは ぜんぶで 何こ あるでしょう。」という文章題に対して，3×5でも5×3でもよいという主張にはならない，ということです。

はじめに，作成した図を：

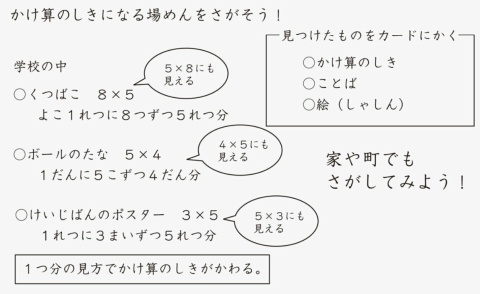
　「映像」と「右のような場面」について，それぞれ写真があるのですが引用では省略しています。右のような場面というのは，壁の掲示物で，3段・4列に並んでいます。こちらについて，冒頭で示した画像の左列のように，「●」を用いて構成することができます。それを列ごとに見れば，1つの列に3個，それが4列あるという分け方ができ，このとき，式は4×3＝12となります。また，段ごとに見れば，1つの段に4個，それが3列あるという分け方になり，式は3×4＝12です。
　団子を含む映像のほうは，クォータービューによる団子のアレイと見ることもできますが，掲示物と異なる点があります。串にささっているのです。「串が3本あること，団子が4個ずつ並んでいることを見いだせば」，1つ分の数は4，いくつ分は3がそれぞれ対応し，式は4×3＝12です。
　この団子の並びでは，3×4＝12と式に表すことが期待されていません。これは冒頭の画像からいくつかを隠した（使用しないようにした），次の画像で説明ができます。

　「1つ分の数は3，いくつ分は4」と認識したときに，そこから，囲い込みのないアレイや，「1つ分の数は4，いくつ分は3」の場面に移動することは，『小学校学習指導要領解説算数編』や，小学校算数の教科書・書籍・学習指導案などから読み取れる状況をもとにすると，期待されていないのです。


『誰もができる子どもに活用力をつけるワクワク授業づくり―第2回RISE授業実践セミナーの報告』p.69です．公開授業の「展開」として書かれたうちの一部で，授業前に作成しておく，学習指導案に似た記述です．
授業者は夏坂哲志氏で，一つ前の項目で挙げた書籍の監修者です．
図ですが，これもまた，枠を取り除けば，デカルト積が見えてきます．
このページで，考えさせられたのは，図と，最初に提示する「文」との対比です．問題文は「はこが、4はこあるよ。それぞれのはこには、あめが3こずつ入っているよ。」であり，合わせて，総数は12個であることを先に明示しています．総数を求めるのではなく，求めるための式を作る，という授業です．
当初は「図と言葉とで，表しているものが違う」という認識だったのですが，今ではその理由・区分けが明確です．その文は，倍の乗法です．それに対して図は，積の乗法です．ということでここにも，倍の乗法と積の乗法の混同が見られたのです．
問題文に対して，「4×3」ではいけない，「3×4」と書けるよう指導することの議論は，p.70からの授業協議会で，諸氏の発言から読むことができます．アメリカでは4×3になるという発言もあって，これについては「一種の約束事ですよね」(p.77)によって区切りをつけ，公開授業に話を戻しています．


　本記事は，以下の記事を改訂したものです。以前に書いた記事の抜粋を追加したほか，リンク先を変更したり，現在アクセスできない情報はその旨を説明したりしています。

*1:https://erid.nier.go.jp/files/COFS/h29e/chap2-3.htm

*2:「倍の場面」「積の場面」を，用語として，学校で学ぶわけではありません。わり算の「等分除」「包含除」も同様です。それぞれに該当する場面を通じて，かけ算・わり算の式で表せることを学びます。

*3:https://takexikom.hatenadiary.jp/entry/2019/09/10/211914，https://takehikom.hateblo.jp/entry/2022/05/10/235959

*4:https://takehikom.hateblo.jp/entry/2022/12/29/062637およびhttps://takexikom.hatenadiary.jp/entry/2022/12/29/062638で取り上げている文章題も，ここに分類されます。

*5:https://doi.org/10.32296/jjsmep.50.6_74よりPDFファイルがダウンロード可能な文献では，「こどもは，結局，9個ずつのグループが6つとして答を求めるくふうをする」「男の子1人について5組ずつになるリストを作って，結局，5＋5＋5という累加で答を求める」とあります。