3×4と4×3，答えは同じだけど，意味は違う（令和2年版）

　以下の本のp.38，2年のかけ算の授業展開です。

発問で見る 数学的な見方・考え方を働かせる算数授業 実践編

　画像の左にある，児童(C)・教師(T)のやりとりは，次のとおりです。

T では，この12個を同じ数ずつに並べ直して，かけ算の式になる図にしてみましょう。
C ぼくはこんな図（上図*1）にしました。
C 3×4＝12だね。
C えっ，4×3＝12だよ。
T どちらの式が正しいのでしょうか?
C だって，3×4の式だったら，3が4個という意味だから，図が違うよ。
C 4が3個という図だから，4×3＝12がが*2正しいです。
T 答えは同じでも，図が違うということですね。
C 「同じ数がいくつ分か」というかけ算の意味を考えないといけないね。
C 他にもできたよ。

　このページには，絵が5つあります。いちばん上は，3個と4個と5個の●です。教師は「この12個を同じ数ずつに並べ直して，かけ算の式になる図にしてみましょう。」と指示しています。2枚目と3枚目は冒頭の通りで，「他にもできたよ。」という図は，2×6＝12を表し，最後の絵は，12個を横長の丸で囲っており，式は12×1です。アレイ（長方形的配列）は次のページにありますが，1つ1つを丸で囲って（見た目は二重丸が12個），式は1×12です。
　冒頭の下図は，3×4＝12と，4×3＝12の違いを表したものとなっています。算数の式としては「3×4＝12」「4×3＝12」ですが，いずれにも，かけられる数の右下に「が」，かける数の右下に「こ」を添えて，2つの数が何を表すのかを区別しています。
　2年のかけ算の授業で，図示しながら，a×bとb×aの違いを理解するというのは，今年出版の他書にも載っていました。

　次の本のp.25です*3。

板書＆イラストでよくわかる　３６５日の全授業　小学校算数　２年下 (板書&イラストでよくわかる)

　このように，「図で根拠を示すこと」「かけられる数とかける数の違いを確認すること」は，今年に顕著な傾向というわけではありません。かつて以下のように，スライドを作ったことがあります。

　このスライドはhttps://www.slideshare.net/takehikom/23-32-123835241/42を切り出したものです．初出はhttps://www.slideshare.net/takehikom/ss-45239765/44*4です。
　同じ意図の図はhttps://f.hatena.ne.jp/takehikom/20111130060704とhttps://f.hatena.ne.jp/takehikom/20140206065450で，当ブログではそれぞれ小学校学習指導要領解説算数編と合わせて読みたい，2010年・2011年の文献とかけ算の「順序」について（2017.12）で紹介しています。
　今年出版のまた別の本では，「一つの場面に対して，かけられる数とかける数を交換した2つのかけ算の式で表せること」が特徴的でした。

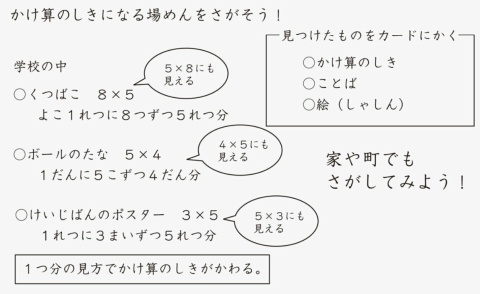
　これらは，次の本のp.29とp.37です。板書の一部であるのに加え，2の段などの九九を学習する前の授業となっています。

板書で見る全単元・全時間の授業のすべて　算数　小学校2年下（板書シリーズ）【電子版・DVD無しバージョン】

　ただしこれらのかけ算の式も，「1つ分の数×いくつ分」に基づいています。2×3と3×2などの式の違いは，それより前のpp.26-27で学習しています。
　「一つの場面に対して，かけられる数とかける数を交換した2つのかけ算の式で表せること」については，今年度から使用の，東京書籍の算数教科書にも見ることができます。

• 新しい算数 | 2年度用 小学校教科書のご紹介 | 東京書籍

　「3年上p.2～3」ですので，3年の算数の最初の授業（授業開き）となります。20個の黄色の丸を，太さ2の十字型に配置しています。しほさんは，5個のまとまりを4つ作って，式は5×4＝20，答えは20こです。こうたさんは，4個のまとまりを1つだけ囲っていて，式は4×5＝20，答えは同じです*5。
　「かけられる数とかける数を交換した2つのかけ算の式で表せる」について，どのような場面でも交換できることは意図されていませんし，交換可能な場面はいずれも，図として提示されています*6。「さらが 5まい あります。1さらに りんごが 3こずつ のって います。りんごは ぜんぶで 何こ あるでしょう。」*7という文章題に対して，3×5でも5×3でもよいという主張にはならない，ということです。

　メインブログ（わさっきhb）の「答えは同じだけど，意味は違う」は：

• □×△と△×□，答えは同じだけど，意味は違う（2013年版）
• 2×3と3×2，答えは同じだけど，意味は違う（2014年版）
• 4×3と3×4

*1:原文では「右図」

*2:原文ママ

*3:ひとつめくったp.27では，6個ずつ5皿のときのかけ算の式「6×5＝30」と，「どうして，5×6ではいけないの?」という疑問文，そしてそれを解決するための図が，黒板の中央に位置しています。ページ下段（黒板に見えないところ）では，「どうして，この式は5×6ではいけないのかな?」という問いかけに対し，「だって，5×6だったらたこやきが5個の皿が6皿あることになります。」という答えが，イラスト化されています。

*4:http://d.hatena.ne.jp/takehikom/20150228/1425073124

*5:この場面（丸の並び）は，https://takehikom.hateblo.jp/entry/20111017/1318783204で取り上げていまして，そこで参照した本では，4×5になる囲み方（原文では「4×5が見えるよ」）が先，5×4（「5×4が見えるよ」）があとです。

*6:『板書で見る全単元・全時間の授業のすべて 算数 小学校2年下』p.37の「くつばこ」「ボールのたな」「けいじばんのポスター」は，発表（板書）としては言葉のみですが，それぞれの場面がアレイに対応付けられることは容易に想像できます。左のページの板書に書かれた3つの事例には，「～にも見える」の吹き出しがなく，アレイに対応させるのが困難な状況と考えられます。

*7:本記事で紹介した，今年出版の3冊のいずれにも，このタイプの文章題は見当たりませんでした。