かけ算の順序の昔話

算数教育について気楽に書いていきます。

四則の単項演算・二項演算について

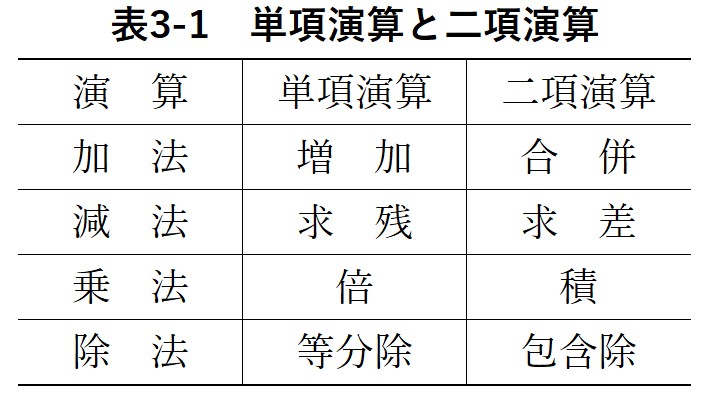
　小学校算数に関する2冊の本で，四則計算を単項演算と二項演算に分ける表が掲載されていました。

　先の表は，志水廣(編著)『小学校算数科の指導』p.54，あとの表は算数科教育学研究会(編)『新編算数科教育研究改訂版』*1p.131の内容をもとに，Excelで自作しました．

小学校算数科の指導

小学校算数科の指導

Amazon
新編算数科教育研究改訂版

新編算数科教育研究改訂版

Amazon

　本文はそれぞれ以下の通りです。

（『小学校算数科の指導』pp.53-54，執筆者は黒﨑東洋郎）
① 演算の意味は2つ
　一般に，抽象数では，加法，減法，乗法，除法の四則演算は二項演算とみられている。しかしながら，実際の事象では，四則演算には次の2つの意味をとらえさせる必要がある。

  • 単項演算（unary operation）　（単項演算：a\overset{b}{\to}c）
  • 二項演算（binary operation）　（二項演算：(a，b)\to c）

　算数では，加法や乗法などが用いられる実際の事象で演算の意味を理解させることが大切である。実際の事象では，単純に二項演算だけで片付けられない場合がある。「5個もっていて，4個もらうと，何個になりますか」という問題は，初めに数5が存在し，それに4が作用して，9になるという単項演算（aがbに作用してc）になる。実存する四則演算には，両者の意味があるので，数例の事象により演算の意味を認識させることが大切である。
(略)
② 四則演算
　四則演算のそれぞれの演算には単項演算と二項演算の意味がある。加法の演算には，増加と合併の場合がある。減法の演算には，求残と求差の場合がある。乗法には，倍と積の場合がある。除法には，等分除と包含除の場合がある。実存する四則演算の全てが単項演算と二項演算だけで分類整理できるの*2ものではないが，概ね表3-1のように整理することができる。

（『新編算数科教育研究改訂版』pp.130-131，執筆者は小関熙純）
(1) 演算の意味について
　加法，減法，乗法，除法は，二項演算（bianry operation）である。それは，たとえば，加法
　　　5＋3＝8
では，5と3という2つの数に「＋」というはたらきがあって，8という数が決まってくるということである。
　抽象数については，このようにみるのがよく，上の式も二項演算としての加法を示したものといえるが，小学校においての演算の実際的な意味の指導では，加法や乗法が適用される具体的対象を，はっきりと認識させることが必要で，その場合は，単純に二項演算とかたづけるわけにいかない。たとえば，
　　　「部屋に男子5人，女子3人いる。あわせて何人いるか。」
という問題では，2つの数量5，3から8を導くもので，
　　(5,3)\to 8　　（一般に，(a,b)\to c）
の形の二項演算といえる。ところが，
　　　「部屋に5人遊んでいた。そこへ3人来た。あわせて何人か。」
という問題になると，これは，はじめに5があって，それに3が作用して8になるということで，
　　　5\overset{3}{\to}8　　（一般に，(a\overset{b}{\to}c)）
の形の演算，つまり，単項演算（unitary operation）と見られる。
　実在する四則計算のいっさいを，単項演算か二項演算かだけで割り切るのは，おおざっぱすぎるかもしれないが，とにかくこの両様が考えられ，具体的な意味づけをすると，右のようになる。
　演算記号の導入の段階で，両様の具体例をいくつかずつ与えて，演算の意味をしっかり認識させることが大切である。

　2つの文章を見比べると，「抽象数」「片付けられない／かたづけるわけにいかない」「a\overset{b}{\to}c」*3といった共通の表記があるのがわかります．表の扱いについても，「実存する四則演算の全てが単項演算と二項演算だけで分類整理できるのものではないが／実在する四則計算のいっさいを，単項演算か二項演算かだけで割り切るのは，おおざっぱすぎるかもしれないが」で類似しています．その一方で，「四則演算／四則計算」「unary operation／unitary operation」といった違いも見てとれます。
　現時点では，新しい本が古い本に依拠して書いた可能性だけでなく，別の出版物に記載があって2冊ともそこに依拠する可能性も，否定できません。
　「単項演算」という名称こそ使用していないものの，2つの数の間に矢印をかいて「10倍」または「×10」などを添えるのは，今の教科書でも高学年で活用されています。

　本記事は未完成です。関連情報を以下に並べておきます。

*1:奥付のページに「本書は、2010年に学芸図書より刊行したものです。」とあります。

*2:原文ママ

*3:本記事ではTeX記法を使用しているため，矢じりの形状は「＞」ですが，参照した2冊とも「▶」でした。