東京都算数教育研究会(都算研)が2019/11/17付けで,平成30年度に実施した学力実態調査の結果を公表しました。
以下よりPDFファイルがダウンロードできます。
平成30年度実施分では,都算研のホームページに,依頼文書のほか,集計のExcelファイルがリンクされており,そこから,各校での集計における正誤の判定基準などを知ることができました。
実施依頼の時点で,気になったことを,500-(x×80)は間違いに取りまとめていました。そこでこの誤答の出題となっている,第6学年大問7を,「結果及び考察・H30年度」で見てみました。
問題文は以下のとおりです。ふりがなは書き出していません。「つり求める式を書きましょう」は原文ママです。
7 次の文章にあてはまる式を、xを使って表しましょう。
(1) 1個80円のチョコレートをx個買って、500円を出しました。つり求める式を書きましょう。
(2) 80gの入れ物に、1個20gのボールをx個入れました。重さを求める式を書きましょう。
このうち(1)の正解例として,解答欄には「500-80×X,500-(80×X)」とあります*1。そして出題の下の「評価基準及び割合」の表について,この問題の評価基準は「A 正答」「C1 500-(x×80)」「C2 80×x-500」「C3 左記以外の誤答・無答」となっています。
右の帯グラフの平成30年度分を見ると,パーセンテージは70,15,24です。500-(x×80)と書いたのが15%というのはおかしいと思いながら,よく見ると,「15」にはC2に対応する網掛けが施されています。
ということでC1は「記録なし」で,有効数字を1%(それ未満は四捨五入)と仮定しても,0.5%に満たないということになります。平成28年度の帯グラフも同様です。
2年連続この結果ですので,「C1 500-(x×80)」という基準は不要と思われます。xという文字と,乗算記号とをきちんと書き分けて,適切な式を立てることができるかという観点では,2月に指摘した,「500-80x」「500-80×」の解答を集計すべきではなかったかとなります。
2つの小問はいずれも,正解に「×x」の表記が含まれますが,それらを書かせること(「×」と「x」を区別して書くのが正解)の妥当性と,(1)では「かけ算の順序」で正誤が異なるのに対し(2)で「たし算の順序」は問わないという,正誤判定の一貫性も,気になります。
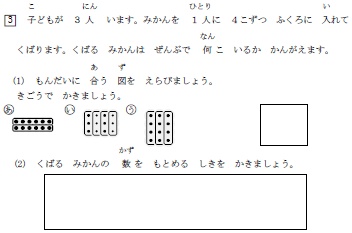
第2学年大問3に移ります。PDFでは解答欄に正答例が書かれていますが,それらを白にした「問題」は,以下のとおりです。
「子どもが 3人 います。みかんを 1人に 4こずつ ふくろに 入れて くばります。くばる みかんは ぜんぶで 何こ いるか かんがえます。」という問題文と,「(1) もんだいに 合う 図を えらびましょう。きごうで かきましょう。」「(2) くばる みかんの 数を もとめる しきを かきましょう。」は,公表されている前回(H26年度)と同一です。
しかし違いもあります。図が三択になっています。(あ)を,今回新たに入れています。
分析には「図を正しく選べた児童は、前回調査時より7ポイント下がっていた」とあります。この7%分が全員,(あ)を選んだというわけではないでしょうが,選択肢を増やすと正答率が下がるのには仕方のないところです。個人的には以前の二択のほうが,「理解過程」と「解決過程」の度合いを知るのにより良いと考えます。
ところでこの大問は小問2つで構成されていますが,「評価基準及び割合」では以下のとおり,組み合わせて細分化しています。
- A 完答/45%
- B1 (2)のみ正答/7%
- B2 (1)のみ正答 (2)3×4/21%
- B3 (1)のみ正答 (2)3×4以外/8%
- C1 (1)誤答 (2)3×4/8%
- C2 左記以外の誤答・無答/11%
小問ごとの状況を,集計してみました。
- (1)の正答率:45+21=66%
- (2)の正答率:45+7=52%
- (1)の正誤にかかわらず(2)で3×4を書いた割合:21+8=29%
なお29%という数値は,分析の文章に「29%の児童が問題文から安易に立式していることが分かった」と書かれています。この出題に関して,都算研としては外在的評価,また実施の各校としては2年の学習内容に関する総括的評価と見なすことができますが,3年のはじめに授業で提示して復習に使う---「3年のかけ算」を学習していく前の,診断的評価とする---のも有望に思います。「5万人が受けたテストで,1万5千人くらいが,式に3×4って書いたんですよ!」と付け加え,3×4と4×3の対比をするのがよいでしょう。
あとは気になったところを個別に書いていきます。
- 第1学年大問7は,「この年より問題の一部を変更して実施している問題」ですが,正答率が大幅に下がっています。グラフを批判的に見るということに発展できる,良問だと思います。
- 第2学年大問5について,集計用紙(xls)に書かれている「1×30,30×1は、乗法の式になっているが数えていると考えられるので、正答としない。」は,評価基準の表と分析のいずれにも記載されていません。
- 第5学年大問6の分析(というか解説)に,いらすとやの先生の絵があってびっくりしました。
- 数直線(「二重数直線」「比例数直線」とも呼ばれる図です)を問題に出したのは第6学年大問2で,従来からの改題です。分析では「前回の立式に加え今回は、問題に合った数直線を選択する問題を追加した」とありますが,今年2月の記事で見てきたとおり,公表されていない平成28年度は,数直線をかかせる問題だったと推測できます。評価基準及び割合について,「B 数直線× 立式○」の割合は,(1)では2%,(2)には記載なし(多めに見積もっても0.5%未満)です。
- 数直線を解説に使用するのは,何か所か見られます。矢印に添える関係は「×3.5」や「
倍」など,かけるものばかりですが,第6学年大問3解説の「□÷
の数直線」には「÷
」を入れるほうがいいのではと思いました。
上記のうち「理解過程」「解決過程」,それと「外在的評価」「総括的評価」「診断的評価」については,メインブログの以下の記事で整理しています。
URLから分かるとおり2015年の記事です。きっかけは,今回の第2学年大問3の問題について,平成24年度実施時に,問題に合う図を選ぶ小問が入ったことでした。今回の変更は,上で述べたとおり個人的には適切と思っていませんが,都算研の2年ごとの(数と計算・数量関係を対象とした)学力実態調査の出題と解答状況から,学ぶことは多いと考えています。
若柳小学校から切り離して,どのような出題が「かけ算の意味」を問うものとしてふさわしいか,時間をとって整理できればと思っています。
*1:Xが大文字になっているのは,報告と問題の作成者間で連携が取れなかったためと考えられます。問題文と,訂正版の実態調査集計用紙に見られる「x」は,Times New Romanの斜体指定なのに対し,報告の分析において,「□がxの」のxは,日本語フォントの斜体字に見えます。