- 笠井健一: 全国学力・学習状況調査から見えてきたもの, 算数授業研究, 東洋館出版社, Vol.130, pp.36-39 (2020).
「解説資料」と「報告書」の違いを,確認しておきます。解説資料は実施直後に問題・正答例と合わせて公開され,出題意図や(集計前の)解答類型などが書かれています。それに対し,報告書には集計(各類型が何パーセントかなど)や,正答率などに応じた指導に関する提言が入っています。
今回見た分の参考文献では,解説資料は令和2年度までありますが,東日本大震災と新型コロナのために実施・集計しなかった平成23年度と令和2年度の分は,報告書の記載がありません.なお最後の一つ前の行には「平和元年度」という誤記も見られます。
問題例より前,pp.36-37に合計3つの表があり,表見出しは順に「観点別設問数と平均正答率」「AB問題別正答率の分布」「問題形式別正答率の分布」です。後二者の表は,「90%以上」「80%以上90%未満」...「0%以上10%未満」を各行の左の列に置き,正答率がそれぞれに該当する出題数をカウントしています。
問題例では,平成19年度のA5(A問題の大問5,以下同じ)とB5,平成20年度のA5,平成20年度のA6,平成24年度のA3,平成30年度のA2,平成22年度のA2,平成30年度のA7,平成30年度のA3を取り上げています。「平成20年度のA6」以降は,A問題で正答率が50%未満とのことです。一つだけB問題を挙げているのは,縦と横の長さが書かれた平行四辺形の面積はほぼ間違えなく求められているのに,それと同じ形の公園の面積を求めて説明する問題の正答率が著しく低いという事例になっていました。
この前後のページで,さまざまな著者が取り上げている問題の実施年度と出題概要を,箇条書きにします。
- p.16: 平成31年度の2(洗顔と歯みがきで使う水の量)
- p.19: 平成19年度のA1ほか(基本的な計算)
- p.21: 平成26年度のA6(平行四辺形が作図できる理由)
- p.24: 平成20年度のA6(重さや面積についての感覚)
- p.26: 平成25年度のA5(計器の選択)
- p.26: 平成29年度のA4(任意単位を用いた測定)
- p.40: 平成27年度のB2(洗剤の量)
ここで事例から離れます。「正答率」(「通過率」とも)について,架空の表を作ってみました。
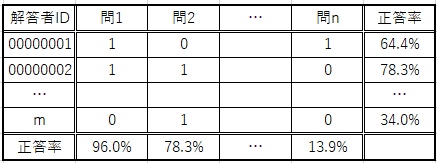
上下端を除き,表の各行は,解答者ごとの情報です。解答者00000001は,問1は正解(1),問2は不正解(0),...,問nは正解で,正答数を問題数で割ることで,この解答者の正答率が求められます。
左右の端を別にして,列ごとに見ることもできます。問1については,解答者00000001は正解,解答者00000002も正解,...,解答者mは不正解で,正答者数を解答者数で割ることで,この問題の正答率を求めるわけです。解答者00000002の正答率も,問2の正答率も,「78.3%」と値は同じですが,意味は異なります。
算数授業研究Vol.130の特集で,全国学力・学習状況調査の出題をもとに「つまずき」と書かれているのは,例外なく,問題ごとの正答率(表の最下段)を見たときに,低い値になっている出題と,結び付けられています。
解答者数が多く,同じように解答ごとに正答率などを求めて分析や対策とともに公開しているテスト事例には,東京都算数教育研究会の学力実態調査があります。都算研 データ室TOPより,見ることができます。
ところで,全国学力・学習状況調査では,報告書で「集計結果(正答等の状況)」という項目で,児童数・平均正答数・平均正答率などを記載しています。これは上の表でいうと,右端の列の値に基づいています。
全国学力・学習状況調査の批判で見かける「学力」も,行ごとに算出される件と関連づけられるように思います。去年と今年に出版された2冊の本を読んで,強く感じたのでした。
「解答者の正答率=正答数/問題数」「問題の正答率=正答者数/解答者数」という算出方法でよいのかという問題意識を持ったとき,代替手法として有望なのは,項目反応理論の適用です。上のように「1」と「0」の値で正解・不正解の表(項目反応パターン)にを作っておけば,ソフトウェアを使って処理することで,正答率とは異なる数値が求められます。例えば解答者の正答率に置き換わるのは,能力値であり,問題の正答率のほうは識別力・困難度になります(能力値・識別力・困難度のいずれも負の値を含む実数値です)。メインブログ(わさっきhb)より,2件にリンクします。


