比例の表から2πrへ

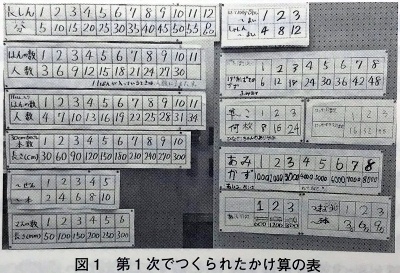
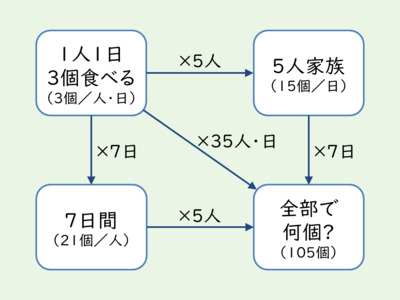
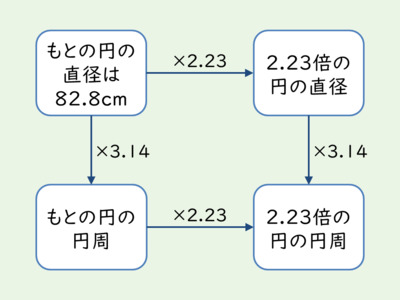
　「数学の公式では円周の長さは2πrである。賢い子供なら、すでに公式を知っていて、それに従い「2×3.14×3」と書いてもおかしくない」（円の円周を，円周率を使った式で表す）から，話を始めます。小学5年の算数で，「半径3cmの円の円周の長さを求めなさい」という問題に対し，「2×3.14×3＝18.84　答え18.84cm」と，式と答えを書く子がいたとします。どうしてその式になるのと先生が尋ねたときに，l＝2πrだからと言う説明で，先生が，またはクラスの子どもたちが，納得してくれるのかは，分かりません。
　なぜ2πrであるのか，言い換えると，なぜ2πrと表せるのかというと，中学1年で学習する，「文字を用いた式」を使うことになります。現行の『中学校学習指導要領解説数学編』では「文字を用いて数量の関係や法則などを式に表現するとき，乗法の記号×は，文字と文字の間や，数と文字の間では普通は省略し，除法の記号÷は，特に必要な場合のほかは*1，それを用いないで分数の形で表すことを学習する。」と書かれています。このルールにより，円周＝半径×2×円周率という言葉の式（小学校で期待される式）について，円周をl，半径をr，円周率をπの文字で表したとき，l＝2πr（中学校で期待される式）が得られるという次第です。なお，かけ算の式の小中連携に関しては，4a+3bの3例で事例を紹介しています。
　「円周＝半径×2×円周率」を直接用いることなく，l＝2πr，または「円周＝2×円周率×半径」を得ることも可能です。対応表を作ります*2。2行で構成し，上の行は半径，下の行は円周です。具体的に半径1cm，2cm，…，の円を描いて，それぞれの周の長さを測定し，次の表を得たとします。

半径(cm)	1	2	3	4	…	10	…
円周(cm)	6.28	12.57	18.85	25.13	…	62.83	…

　どの列も，円周÷半径が6.28に近い値となります。商一定ならば，これらの量は比例の関係にあることを意味し，この商が比例定数となって，円周＝6.28×半径となります。半径をx，円周をyとすれば，y＝6.28×xです。
　もちろんこの6.28は，円周率の2倍のことです。ともあれ，関係を表す式としては「y＝6.28×x」にとどめておき，この6.28は中学校では2πと書くんだ，かけ算の記号も書かないんだとまで言えば，最終的に「y＝2πx」という等式に至ります。
　小学校の算数の考え方で*3，2πrと同等の式を導けるわけですが，実際に小学校でこのような学習をしているわけではありません。学習に使用されているのは，「半径と円周」ではなく「直径と円周」の関係です。その場合でも2行の表にすれば，商一定なのが分かりますが，これは「円周の直径に対する割合（がどの円でも同じ値になること）」を意味し，「円周率」の導入へとつながるわけです。
　また別の観点で，小学校ではなぜ「円周＝半径×2×円周率」であって「円周＝2×円周率×半径」は採用されないのかを，書いておきます。上に示した，2行の対応表について，上下どちらも単位がcmで，同種の量となっています。この場合，「もとにする量×割合＝比べる量」の関係式で表現できます*4。円周÷半径＝（円周率の2倍）であり，（円周率の2倍）が割合に対応します。半径を「もとにする量」，円周を「比べる量」にそれぞれ，対応づければ，「半径×（円周率の2倍）＝円周」になるという次第です。
　それに対し，「円周＝2×円周率×半径」と書いてみたとき，「×半径」が何をするかけ算なのか，（比例の式を学習していない）小学生向けの解釈は思いつきません。
　これは8×3を，表から見つけるで紹介した事例と，対比をなしています。図3は以下の通りでした。

はんの数	1	2	3	4	5	6	7	8	9	10
人数	3	6	9	12	15	18	21	24	27	30

　この場合，「3×はんの数＝人数」という式が期待されます。3は，1つの班の人数を表します。5年の「乗法の意味の拡張」（子どもたちがこの用語を学習するかどうかはさておき）にもとづくと，「×はんの数」は，人数そのものをかけるのではなく，3人の班が1つだけなら3人，n班なら3人のn倍，と解釈することになります。
　この「はんの数」と「人数」の関係では，「はんの数×3＝人数」と表現することに難点があります。2年では指導されておらず，4年の「伴って変わる二つの数量」が必要となります。2つの量が異なる種類の量であり，半径または直径と円周との対応表との相違点となっています。

*1:次期の解説では，「のほかは」は「を除き」に変更されています。

*2:現行の『中学校学習指導要領解説数学編』のPDFで「π」を検索すると，「例えば，比例に関して，半径がrで周の長さがlの円について，「半径を2倍，3倍，…にすると，周の長さはどのように変化するか」を考えるためには，具体的な数で計算して調べることをしなくても，l＝2πrという式の意味を読み取って簡単に説明すことができる。」が見つかります。次期の解説にも同趣旨の文があります。

*3:ただし「比例」は6年で学習します。円周率や円周は5年です。

*4:「もとにする量」「比べる量」の用語はhttp://www.shinko-keirin.co.jp/keirinkan/sansu/WebHelp/05/page5_23.htmlによります。『小学校学習指導要領解説算数編』ではそれぞれ「基準にする大きさ」「割合に当たる大きさ」と書かれています。B×p＝Aと表した場合には，Bはbase，pはproportion，Aはamountの頭文字となります。

小数・分数のかけ算を何年で学習するか

　現行および次期の学習指導要領では，「小数×整数」は第4学年，「小数×小数」は第5学年の学習内容となっています。分数のかけ算や，速さ，円（円周率，面積）とともに，これまでの学習指導要領ではどの学年に配当されているかを，整理してみました。

　これまでの分については，学習指導要領データベースインデックスを参照しました。戦後まもなくのものもありますが，現行と同形式となっている，1958年（昭和33年）以降を，今回の調査対象としています。それぞれの算数の節について，リンクのあと，学年ごとに（今回の調査で関心のある）学習事項を並べました。なお，同一学年の列挙について，必ずしも各情報源の記載順ではありません。

• 1958年（昭和33年）告示，1961年（昭和36年）施行*1
  • 第3節 算数
  • 4年：小数×整数
  • 5年：小数×小数，分数×整数，速さ，円周率，円の面積
  • 6年：分数×分数
• 1968年（昭和43年）告示，1971年（昭和46年）施行
  • 第3節 算数
  • 4年：小数×整数
  • 5年：小数×小数，分数×整数，速さ，円周率，円の面積
  • 6年：分数×分数
• 1977年（昭和52年）告示，1980年（昭和55年）施行
  • 第3節 算数
  • 4年：小数×整数
  • 5年：小数×小数，分数×整数，速さ，円周率，円の面積
  • 6年：分数×分数
• 1989年（平成元年）告示，1992年（平成4年）施行
  • 第3節 算数
  • 4年：小数×整数
  • 5年：小数×小数，速さ，円周率，円の面積
  • 6年：分数×分数
• 1998年（平成10年）告示，2002年（平成14年）施行
  • 第3節 算数
  • 5年：小数×小数，円周率，円の面積
  • 6年：分数×分数，速さ
• 2008年（平成20年）告示，2011年（平成23年）施行【現行】
  • 第3節 算数
  • 4年：小数×整数
  • 5年：小数×小数，分数×整数，円周率
  • 6年：分数×分数，速さ，円の面積

　次期については，文科省サイトよりダウンロードできるPDFファイルを参照しました。上記と同じ形式にしておきます。

• 2017年（平成29年）告示，2020年施行【次期】
  • 第3節 算数
  • 4年：小数×整数
  • 5年：小数×小数，速さ，円周率
  • 6年：分数×分数，円の面積

　いくつか，補足します。「分数×分数」と書いたときの「分数」は整数を含みます*2。「分数×分数」があり，それより下の学年に「分数×整数」がないものは，「分数×分数」を学習する学年で，「分数×整数」も学習することが想定されます。「小数」についても同様です。わり算は今回，とくに取り上げませんでしたが，「小数×整数」と同じ学年で，「小数÷整数」や，「整数÷整数で商が小数になる場合（割り進み）」も学びます。「円周率」に関しては，「円周」の意味や求め方も合わせて学習します．
　箇条書きにしてみると，昭和では変化がなく，平成に入って，“いじっている”のが見てとれます。昭和のころおよび現行では，「小数×小数」および「分数×分数」をそれぞれ学習する際，一つ下の学年で，かける数が整数の場合を学習することとなっています。平成に入ってからは，現行を除き，「分数×整数」と「分数×分数」は同学年です。また，「ゆとり教育」と揶揄されることもある，現行の一つ前の学習指導要領では，「小数×整数」と「小数×整数」も同学年となっています。
　なお，同じ学年であっても，「かけ算の順序はどっちでもいい」ことを意味しません。実際，1998年（平成10年）告示の第3節 算数について，小数の乗法の記載は以下の通りとなっており（主要部のみ抜粋），「乗数や除数が整数である場合の乗法及び除法」と「乗数や除数が小数である場合の乗法及び除法」が異なる項目となっています。

〔第５学年〕
２　内　　容
Ａ　数と計算
(３)　小数の乗法及び除法の意味について理解し，それらを適切に用いることができるようにする。
ア　乗数や除数が整数である場合の乗法及び除法の意味について理解すること。
イ　乗数や除数が整数の場合の計算の考え方を基にして，乗数や除数が小数である場合の乗法及び除法の意味について理解すること。

　当時の『小学校学習指導要領解説算数編』*3では，アとイは次のように具体化されていました(pp.131-132)。

　a. 乗数, 除数が整数の場合の乗法, 除法の意味（ア）
　乗数，除数が整数である場合についての小数の乗法，除法の計算の指導では，その計算の意味を，整数の乗法「（整数）×（整数）」や，整数の除法「（整数）÷（整数）」を基にして考えることができるようにする。そのためには，乗法における積の小数点の位置や除法における商の小数点の位置などについて，整数の場合と比べながら学習できるよう配慮する。
　整数に小数を乗除する計算の仕方を考える上で,数の相対的な大きさの見方が有効に働く。例えば，1.2×3の計算では，1.2を0.1が12個あるとみて，0.1×（12×3）のように考えることができる。
　b. 乗数が小数の場合の乗法の意味（イ）
　整数の乗法は，様々な場面を利用しながら，次第に，一つ分の大きさを知ってその幾つ分かの大きさを求めたり，何倍かの大きさを求めたりする計算として意味付けがされてきている。
　この学年では，乗数が小数の場合にも,乗法を用いることができるようにしたり，除法との関係も考えて，より広い場面や意味に用いることができるように一般化していく。その際，数量の関係が同じ場面では，整数の場合に成り立つ式の形は，小数の場合にも同じように用いていくという考えにより，小数の場合の式をつくっていく。
　例えば，1メートルの長さが80円の布を2メートル買ったときの代金は，80×2という式で表せる。同じように，この布を2.5メートル買ったときの代金は，80×2.5という式で表せる。
　こうしたことから，整数や小数の乗法の意味は，（基準にする大きさ）×（割合）=（割合に当たる大きさ）とまとめることができる。

　なぜ「×整数」を，「×小数」や「×分数」と分けて（あるいはより下の学年で）学ぶようにしているのかというと，思いつくのは「累加」です。「0.1×3」と「×6」は，それぞれ「0.1が3つ」「が6個」と考えれば，「0.1＋0.1＋0.1」「」と表すことができ，たし算で（手間はさておき）計算ができます。かける数が乗数になると，累加で表せなくなり，そこで乗法の意味の拡張*4が意図されているわけです。
　「3×0.1」や「6×」といった式に表したり，計算して0.3や4を得たりするのは，今回の調査範囲ではいずれも，それぞれ第5学年と第6学年での学習です。ここで，3×0.1＝0.1×3＝0.3のような計算の仕方については，小数の乗法において交換法則が成立することを確認してからとなります。次期の『小学校学習指導要領解説算数編』で「そこで実際に120×2.5を今までに学習した乗法の性質を用いて答えを出してみて，実際の値段と一致するか確かめてみることが大切である。例えば乗法の交換法則を用いて答えを出すと，120×2.5＝2.5×120＝300となる。」と書かれた箇所について，小数の乗法の交換法則を先取りしているように読めます。

*1:http://www.nier.go.jp/guideline/s33e/chap3-3.htmの施行期日（但し書き），およびwikipedia:学習指導要領より，実質的に「1961年度（昭和36年度）」からの施行と判断しました。

*2:小数と分数を含んだ式の計算については，今回参照したいずれにも記載がありませんでした。

*3:isbn:9784491015507

*4:メインブログより：http://d.hatena.ne.jp/takehikom/20120301/1330547942，http://d.hatena.ne.jp/takehikom/20151210/1449694799，http://d.hatena.ne.jp/takehikom/20161122/1479743916

掛け算の順序とは、ニセ科学批判の最後の避難所である

掛け算の順序とは、ニセ科学批判の最後の避難所である #掛算

— takehikom (@takehikom) March 7, 2018

　サミュエル・ジョンソンの「愛国心とは、ならず者たちの最後の避難所である」*1を改変したもので，内容面では，RikaTan（理科の探検） 2018年4月号*2に掲載された「「かけ算には順序がある」と教える教師たち　正解が×にされる不条理」を念頭に置いたものです。
　「掛（か）け算の順序」に相対するのは，「乗法（かけ算）の意味」であり，「学習者の道を選ぶこと」です。

• 順序の強制か，意味の理解か
• あなたは「批判者」ですか？「学習者」ですか？　～本『QT 質問思考の技術』 - ライフハックブログKo's Style

（公開：2022-01-18 早朝）

*1:https://meigennavi.net/word/02/029492.htm, http://www.jlogos.com/d006/5450321.html

*2:[asin:B079ZTVWJN]

円の円周を，円周率を使った式で表す

• 山本弘: 「かけ算には順序がある」と教える教師たち　正解が×にされる不条理, RikaTan（理科の探検） 2018年4月号（通巻31号）, pp.36-39 (2018).

　Kindle版を購入しました。通して読んで，文句しか付けようのない内容でした。
　全体を通して，情報源が古いのです。RikaTanでは2014年に異なる著者による特別寄稿が掲載されている*1のに，それと今回とで何が違うのか，その間にどのような変化があったのかが，一切記されていません。「その間に」で思い浮かぶのは，昨年公表された，学習指導要領およびその解説なのですが，言及なしです。「現在の学習指導要領では、かけ算の順序に関して特に規定されていない」(p.36)については，小数×整数は4年で，小数×小数は5年で学習することと，整合性がとれません。

RikaTan（理科の探検） 2018年4月号 [雑誌] Rikatan(理科の探検)

　教師とのやりとりが，pp.37-38に見られます。

公式を書いたら×にされる?
　少し前、ニセ科学関連の講演をやったとき、かけ算順序固定を子供に教えている小学校教師に会った。僕が講演の中で順序固定を批判したのがお気に召さなかったらしく、順序固定のメリットを力説する。あいにく、どれもみんな僕の知っていることばかりだったが。
　僕はその際、以前から気になっていた質問をしてみた。
「たとえば『半径3cmの円の円周の長さを求めなさい』という問題の場合、どういう式を書くんですか?」
　するとその教師、「待ってました」と言わんばかりの嬉しそうな表情を浮かべ、ホワイトボードに式や図を描いて自信たっぷりに説明しはじめた---円の面積の求め方を。
　円の面積を求める方法は、説明するのは難しい。おそらくこの教師も、しょっちゅう子供がひっかかってしまうことに手を焼き、説明のしかたをマニュアル化して頭に叩きこんでいたのだろう。そのため、僕が「円の円周を求める問題」と言ったとたん、「いつもの問題だ!」と早とちりしてしまったのだ。
　何のことはない、この教師こそ、「問題文の意味を理解せず」「意味のない式を書いてしまう」人物だったのだ。
　その後、僕に注意されて間違いに気づき、正しい式を書きはじめた。ところが、最初に「3×」と書いた直後、手がぴたりと止まってしまった。次に「2」と書くべきか「3.14」と書くべきか分からなくなったのだ!
　かけ算順序固定派のルールでは、最初に書く字は回答と同じ単位の数字と決まっている。この場合、求めるのは円の円周（cm）だから、当然、最初は3（cm）である。だが、2番目、3番目の数字についてのルールがない。これまでずっとマニュアル通りに問題を解いてきたの「で、マニュアルにない問題を突きつけられたとたん、混乱してしまったのだ。
　その教師は悩んだ末、「3×2×3.14」という「正解」を書いた。しかし、数学の公式では円周の長さは2πrである。賢い子供なら、すでに公式を知っていて、それに従い「2×3.14×3」と書いてもおかしくない。しかし、そう書いたら、かけ算順序固定派の教師に×にされてしまうのだ!

　事実関係において見過ごせないものがあります。「かけ算順序固定派のルールでは、最初に書く字は回答と同じ単位の数字と決まっている。」の文です。算数教科書や学習指導案より，反例を見ることができます。「段数×４＝周りの長さ」の件で，次期の算数解説に取り入られました*2。この事例のほか，長方形・正方形の面積の公式も考慮に入れると，被乗数と積とが異なる種類の量になり得ることは，4年で学習します。円周の長さや円周率よりも前です。「最初に書く字は回答と同じ単位の数字」，言い換えると「被乗数と積は同種の量」というのは，著者が忖度するものではなく，2年および3年の出題・学習をもとに経験的に得られるものです。
　それはそれとして，上記に「円周」が4回，出現することを起点に，話を掘り下げてみることにします。というのも，そのうち3回は，「円の円周」となっています。最初の「半径3cmの円の円周の長さを求めなさい」は，「半径3cmの円」の「円周の長さ」と解釈すればいいのですが，あとの2つの「円の円周」は，単に「円周」でよいはずです。
　「円」と「円周」，それから「円周率」をどのように書いているのか知るため，手元の2冊の紙媒体で，調べてみました。
　まずは『算数教育指導用語辞典 第四版』*3です。出現ページとその記載を箇条書きにします。「//」は改段落を表します。

• p.95: 平面上で，ある定点から等距離にある点の集まりとみられる曲線，または，この曲線の内部を含めた全体の形を円という。この定点を円の中心といい，円をふちどっている曲線を円周という。
• p.100: 5年で，円周の長さと直径の長さの関係を調べ，円周の長さが直径の長さの何倍になっているかを調べさせている。その何倍かを表す数を円周率という。
• 同: [1] 関数の考えを育てる一場面 // いろいろな大きさの円，すなわち，直径（半径）の異なるいくつかの円を並列的に見て，何が変化しているか，逆に，何が変化していないのかに着目させ，直径の長さと円周の長さを変数として見られるようにしていく。
• 同: [2] 測定で円周率の意味を知らせる // 実際にいくつかの具体物で円の直径と円周を測定し，どんな大きさの円についても，円周の直径に対する割合が一定であることを見出すようにする。その体験的な気づきをもとに，指導していく。
• 同: 円周率 // the ratio of the circumference of a circle to its diameter, circle ratio（π） // 円周の長さが直径の長さの何倍かを表す数を円周率という。円周率（π）は，どんな大きさの円でも一定の値をとる。円周率は，詳しくは，3.1415926535897932384626…のようにどこまでも続く。その数の並び方は，循環小数のようなきまりは見られない超越数といわれるもので，わり算で求められる数でない。ふつう3.14が近似値として用いられる。
• p.279: 円の性質 // 円をふちどっている曲線を円周（用語は5年），中心と円周上の点を結ぶ線分を〔以下略〕
• p.309: 円について，円周の直径に対する割合（円周率）が一定であることを知り，円周・直径・円周率の関係を明らかにする。

　2冊目の本は，『算数・数学用語辞典』*4です。

• p.22: 円 えん [circle] // コンパスで描いた曲線が囲む平面の一部を円といいます。また，この曲線を，この円の周といいます。円の周の一部を弧といいます。// コンパスを使わない一般的な定義は次のようになります。// 平面上の1点Oから等距離にある点は，1つの曲線を描きます。この曲線を囲む平面の1部を円といい，点Oを，この円の中心といいます。また，この曲線を円周といいます。〔以下略〕
• p.23: 円周 えんしゅう [circumference] // 円を囲んでいる曲線を，円周といいます。〔以下略〕
• p.23: 円周率 えんしゅうりつ [ratio of circumference of circle to its diameter] // 円周の長さと直径の長さとの比を円周率といいます。円周率は，回りを表すギリシャ語ペリフェレイア〔ギリシャ語のため省略〕の頭文字をとって，π（パイ）で表します。// π＝3.141592653589732384… // が知られています。計算機の進歩によって，現在，その値は2兆桁を超えて計算されています。

　とりあえず，「円の円周」という表記については，どちらの本にも出現しませんでした。「円をふちどっている曲線を円周という」「この曲線を，この円の周といいます」のように，円周の概念の導入にあたっては，書き方に配慮のあとがあるのも，読み取れます。
　Webで読むことのできる情報として，wikipedia:円周を見ておきましょう。簡潔な定義は「円周（えんしゅう、英: circumference）とは、円の周囲もしくは周長のこと。円周と直径の比率を円周率という。」となっています。図の直後には「円の周長cは」，また円周と面積の説明において「円周を円の半径rについて」といった表記も見られます。「円の」が「円周」に係るような使い方には，なっていません。
　教師とのやりとりに戻る前に，円周率について検討しておきます。wikipedia:円周率では「円周率（えんしゅうりつ）は、円の周長の直径に対する比率として定義される数学定数である」と書かれています。『算数・数学用語辞典』では「円周の長さと直径の長さとの比を円周率といいます」ですし，「比」の文字を入れた円周率の定義は，コトバンク*5，goo国語辞書*6，weblio辞書*7でも見ることができます。
　それに対し，『算数教育指導用語辞典 第四版』では，「円周の長さが直径の長さの何倍かを表す数を円周率という」や「円周の直径に対する割合*8」のように，「比」を使用していません。
　もちろんこれは，「比」は6年で学習するので，5年で円周率を学ぶ段階において利用できないことが関係しています。かわりに，「何倍か」や「割合」を用いています。とくにp.309では，割合を学習する中での円周率の扱いが記されています。小数のかけ算・わり算とともに，割合の概念を学習しておけば，図形にも適用できるというわけです。
　「割合＝くらべる量÷もとにする量」により，割合を求めたとき，「くらべる量＝もとにする量×割合」という式が使えます。円を対象とするなら，もとにする量は直径で，くらべる量は円周，そして割合は，円周率です*9。
　教師とのやりとりで著者が与えた問題，「半径3cmの円の円周の長さを求めなさい」について，直径は3cmの2倍ですから3×2と表せます。そして割合の第2用法と，円周率を3.14とすることにより，（3×2）×3.14，または3×2×3.14という式になります。あとは計算なのですが，3.14×6を筆算することで，18.84が求められます。答えは「18.84 cm」です。
　立式の根拠となる，公式（言葉の式）は，「円周＝直径×円周率」と「直径＝半径×2」です。
　ところで，p.38における「数学の公式では円周の長さは2πrである。賢い子供なら、すでに公式を知っていて、それに従い「2×3.14×3」と書いてもおかしくない」は不可解です。小学校では2πrのような，乗算記号を省略した式は扱いません。中学の数学を先取りしている「賢い子供」なら，2πrと学んだ上で，小学校では「直径×円周率」の公式で式を立てることを，想定すべきでしょう。

（最終更新：2018-03-05 晩）

*1:メインブログではhttp://d.hatena.ne.jp/takehikom/20141004/1412352292で取り上げました。Kindle版はasin:B0739MD1JSです。

*2:http://takexikom.hatenadiary.jp/entry/2017/09/11/215947

*3:isbn:9784316802640

*4:isbn:9784490107807

*5:https://kotobank.jp/word/%E5%86%86%E5%91%A8%E7%8E%87-38162：「平面上の円の円周と直径との比の値」

*6:https://dictionary.goo.ne.jp/jn/26415/meaning/m0u/%E5%86%86%E5%91%A8%E7%8E%87/：「円周の、直径に対する比」

*7:https://www.weblio.jp/content/%E5%86%86%E5%91%A8%E7%8E%87：「円周の直径に対する比の値」

*8:現行および次期の『小学校学習指導要領解説算数編』にも，出現します。

*9:言葉の式で表すと，「円周率＝円周÷直径」となります。https://style.nikkei.com/article/DGXMZO80396050S4A201C1000000にも「円周÷直径」が出現します。

単位なしの立式はミスのもと?

• https://twitter.com/yamasati39/status/968061933495640064*1

　「単位なしの立式はミスのもと」には賛同できません。次元解析や組立単位を，小学校の算数に適用することは，個人的にふさわしくないと考えているからです。

　式に単位を入れることについては，メインブログで以前にまとめていたので，取り出しておきます*2。「45人で，講堂にイスを運んでいます。1人が1個ずつ4回運ぶと，みんなでイスは，何個運ぶことになるりますか」という文章題に対し，現在，小学3年生に出題するなら，期待される式は，「4×45＝180」です。
　単位を入れた立式となると，「4個/人×45人＝180個」が考えられます。この式では「個/人」も，一つの単位となります。他の可能性として，「4個×45人＝180個」も，分からないではありませんが算数・数学的に好まれません。かつては「4個×45＝180個」のように，かけられる数と積に単位を明記し，かける数は（問題文では「45人」とあっても）「45」と無名数にする，というスタイルもありました。
　「単位ありの式」は，加減乗除で利用できます。たし算やひき算の式では，どの項も，また計算結果も，同種の量とし，同じ単位をつけます。お花の数なら「2ほん＋3ほん＝5ほん」，人数の増減なら「13にん－8にん＋5にん＝10にん」などです。
　導入時（2年）で学習するかけ算では，「3こ/さら×5さら＝15こ」といった表記になります。かけられる数の単位は「a/b」と書かれ，「3こ/さら」は，1皿にリンゴが3個ずつ乗っている状況などを表します。かける数の単位は「b」で，かけ算により，単位が「a」の量が得られます。これは日本独自というわけではなく，Schwarz*3やKaput*4も，理論化ならびに実際の教育への適用を試みています。それらの文献で，「こ/さら」「さら」「こ」に対応する概念は，dimensionでもunitでもなく，referentと呼ばれます。次元解析*5では通常，対象とする量は連続量ですが，referentにおいては分離量も許されます。
　「3こ/さら×5さら＝15こ」の式をもとにすると，わり算には2種類の式のパターンが考えられます。一つは，「15こ÷5さら＝3こ/さら」のように，1あたり量を求めるわり算です。もう一つは，「15こ÷3こ/さら＝5さら」のように，1あたり量がわる数になる場合です。前者は等分除，後者は包含除に対応します。なお，面積計算や直積の計数では，ここまで書いてきたのと異なるタイプのかけ算となりまして，式に，「/」を含む単位が出現しません。

　「単位なしの立式はミスのもと」については，「立式するときは必ず単位をつけましょう」ではなく，「立式するときに単位をつけて書くと便利ですよ（ミスが減りますよ）」という意味だと考えられます。しかし，そのように解釈するとしても，算数の具体的な問題における適用に関して，十分に考慮されてきたとは思えません。
　例えば，面積や直積などでない，言い換えると被乗数と乗数の違い（非対称性）があるかけ算でも，単位を書くと手間が増え，その一方で式の正しさや計算の用意さを支援しないような場面が考えられます。2年で学習する倍概念がその最初で，例えば，「6cmの2ばい」をかけ算の式で表す場合，「6cm×2ばい」では積の量が不明瞭（「cmばい」は明らかにおかしい）であり，かといって「6cm/ばい×2ばい」と書くわけにいきません。数学教育協議会の方々の著書を読んできた限り，この倍概念については，「6cm×2」と表しており，「3こ/さら×5さら＝15こ」のタイプのかけ算より，学習における優先度が下げられています。
　面積計算においても，4年で学習する正方形や長方形の面積，またそれらの複合図形くらいであれば，「○cm×△cm＝○×△㎠」は有用かもしれませんが，5年の台形で「（2cm＋3cm）×6cm÷2」，6年の円で「3cm×3cm×3.14」と書いてみると，どうでしょうか。そして，これらにおいても組み合わせたり一部をカットしたりした図形の問題まで考慮すると，立式（答案に書くかどうかはさておき）における単位の有用性を主張するにも，限界があるように思います。
　そして，昨年公開された『小学校学習指導要領解説算数編』*6が，「単位ありの立式」の不都合さに拍車をかけます。具体的には，第1学年の「異種のものの数量を含む加法・減法」と，第4学年の「伴って変わる二つの関係」が該当します。
　「異種のもの」は，例えば，「お皿に1個ずつ，コップを乗せていきます。お皿は5枚，コップは7個あります。どちらがいくつ多いですか?」という文章題で，「7個－5枚」と書いてよいのか，よいとしたとき，差となる量をどう書けばいいのか，ということです。
　「伴って変わる二つの関係」について，解説からは「（三角形の数）＋2＝（周りの長さ）」や「段数×4＝周りの長さ」を見つけることができます。前者の式の被加数と和は異なる量ですし，後者の式の被乗数と積も同様です。
　後者はもう少し検討します。「段数を増やしていくと周りの長さがどのように変わるか」の件では，リフレッシュ研修８（変わり方） | 授業がんばりMATHの最も下の図形のように，変形することで，一つの正方形の長さは4cm，それがだんの数だけあるから，「4×段数＝周りの長さ」と表すこともできます。ここで「4」につけるべき単位は，段数の単位と長さの単位をもとに，「だん/cm」と表せます。10段のときの周りの長さは，図や表を用いることなく，「4だん/cm×10だん＝40cm」とできます。

　ただし，『小学校学習指導要領解説算数編』の記載を読む限り，そのように表すことは，望まれていません。「だん/cm」という単位を認めない，というわけではありません。むしろ，小さな段数について，図を描いたり，2行の表にしたりすることで，帰納的に，「段数×4＝周りの長さ」を得ること，そしてこの式を得たら，10段でも100段でも，当てはめて計算すれば求められることが，ここでの学習の意義となっています。

*1:「ツイートは非公開です...承認された場合のみツイートを表示できます」と表示されます。

*2:http://d.hatena.ne.jp/takehikom/20130428/1367096291

*3:http://d.hatena.ne.jp/takehikom/20130312/1363031965

*4:http://d.hatena.ne.jp/takehikom/20111029/1319835106

*5:算数教育における文章題について書かれた中に，"Dimensional Analysis"の語が出現するものもあります。例えばhttp://books.google.co.jp/books?id=Vyl42R9JV1oC&pg=PA197より読めます。

*6:http://www.mext.go.jp/a_menu/shotou/new-cs/1387014.htmより，PDFがダウンロードできます。本記事ではhttp://www.mext.go.jp/component/a_menu/education/micro_detail/__icsFiles/afieldfile/2017/07/25/1387017_4_2.pdfの内容をもとにしています。

8×3を，表から見つける

• 山田剛史: 日常の問題に役立てたかけ算を数学内の問題に役立てる授業, 数学教育学の礎と創造―藤井斉亮先生ご退職記念論文集―, 東洋館出版社, pp.102-112 (2017). isbn:9784491034447

数学教育学の礎と創造-藤井斉亮先生ご退職記念論文集-

　「都内国立大学附属小学校第2学年の児童35名を対象に2016年11月に行われた授業」(p.103)の分析です。タイトルの中の「数学内」というのは，「学習者の立場からすると，日常の問題（数学外の問題）に役立てていたかけ算を様々な数のかけ算の答えを求めるという数学内の問題に役立てるという学習過程を経験することになる」(p.102)という文に出現します。
　数学内の問題に関して，「ねらい」(p.105)には，「23×3」や「23×5」といったかけ算の式が書かれています。いずれも，標準的には3年での学習です。例えば23×3なら，20×3と3×3に分けて計算をしてから加え，69を得ます。「一の位と十の位に分け」ることも，ねらいに含まれており，先取りの感もあります。
　しかし本文を読む限り，20×3あるいは2×3や，3×3の答えを得るのには，九九を使用していません。代わりに活用されているのは，「かけ算の表」です。この授業より前につくられた，かけ算の表の写真が，p.104で以下のとおり，図となっています。

　いずれも，2行・任意列の表です。どの表も，左端の上下には，異なる種類の量の名称が書かれています（「何枚」の「枚」のように，2年では学習しない漢字も，使用されています）。数の並びについて，上段は「1」「2」「3」…となっています。下段は，それぞれに対応する値ですが，マスの数に対する長さ(mm)のように，九九の範囲を超えている数もあります。累加により，右に伸ばしながら数値を入れていったものと推測でき，p.105には「本授業では「同数ふえセット表」と呼ばれている」が，カッコ書きにされていました。
　ページを進めると，「かけ算の順序」の議論がありました(p.107)。

②8×3の答えを求める場面
　教師が8×3の式を示し，学習者たちは答えを求めた。このとき，1人の学習者は積を24と求めるときに図2の丸で囲った箇所を使ったと発言し，もうひとりの学習者は図3の丸で囲った箇所を使ったと発言した。このことから「あの，何枚だと，～ちゃんの折り紙の答え方（図2の答え方）だと，3個目で24って出てるけど」「そっち（図2の答え方）だと，たぶん，みんな言っているのは，3×8しているのかな，と思ってる」と8×3は図3に示されているというかけ算の表現を誤って捉えている意見が出された。そこで教師から8×3は8＋8＋8，8が3こ，であることを伝え，8×3は図2の丸で囲った箇所であることが確認された。

　引用した文のうち，「そっちだと，たぶん，みんな言っているのは，3×8しているのかな，と思ってる」は，ビデオ記録からの文字起こしで，カギカッコのない「8×3は図3に示されているというかけ算の表現を誤って捉えている意見が出された」は，著者による分析と考えられます。「そっちだと…」を言った子は，図3の丸で囲った箇所が8×3だと考えたが，その後の教師の発言により（いきなり否定はしなかったでしょうが）それは誤りと，読むことができます。
　図1，図2，図3のいずれの表にも，共通点があります。「かける数」と「積」との対応表になっているのです*1。「かけられる数」は，明示されていないと言うこともできますし，上の行が1のときの，下の行の値が，実際には「かけられる数」になっています。これらに気づくと，図2の丸囲みは8×3＝24なのに対し，図3の丸囲みからは3×8＝24を，効率よく読み取ることができます。
　ところで図2の上段左に何が書かれているのか，理解するのに苦労しました。どうやら「何こ」です。「何」の下に「～」と縦線があり，「1」と書いてしまったのを，波線で訂正したものと思われます。子どもが書いたのだと解釈すれば，「枚」を用いたことも，納得が行きます。

*1:「上の段×定数＝下の段」という捉え方は，この授業では期待されていません。学習するとすれば4年です：http://takexikom.hatenadiary.jp/entry/2017/09/11/215947。

a×b×cでもa×c×bでもよい

　ある種の「かける順序を問わない場面」について整理します。小学校の算数で出題したとき，式は，a×b×cでもa×c×bでもかまいませんが，aが乗算記号の右に来ることは，期待されていません。

　はじめに考える文章題は，以下のものです。「相似な図形の長さ」の応用題です。

82.8cmの直径の円があります。その3.23倍の直径の円の円周は何cmでしょうか。

　円周率は3.14とします。答えとなる長さだけでなく，式も書くこととします。
　素朴な求め方は，こうです。円周を求めたい円の直径は，82.8cmの3.23倍ですから，82.8×3.23で求められます。そして円周＝直径×円周率を使えば，円周は82.8×3.23×3.14と表せます。
　電卓で計算してみますと，839.77416となりました。答えは839.77416cmです。小数点以下が細かすぎるようにも見えますが，1桁たりともおろそかにしないという方針のもと，計算させるのは差し支えないでしょう。
　別の考え方もできます。82.8cmの直径の円について，先に，円周の長さを式にします。8.28×3.14です。そして，直径が2倍，3倍，…になると円周の長さも2倍，3倍，…になりますので，求めたい長さは82.8×3.14×3.23となります。計算結果（839.77416）は変わりません。
　この文章題は，以下の文献で取り上げられています。「教授学の探究」は大学の紀要と思われますが，著者は小学校教師です。

• 佐藤敬行, 問題づくりを通して乗除演算の意味を考える―「いろいろな文章問題」（小学校5年）の実践から, 教授学の探究, 北海道大学大学院教育学研究科教育方法学研究室, Vol.23, pp.27-54 (2006). http://ci.nii.ac.jp/naid/120000964041 http://hdl.handle.net/2115/13659

　本文に，授業中のやりとりも載っています(pp.31-32)。「　」が先生，『　』が子どもの発言として読めば，話が合います。

「（2）の式は?」『82.8×3.14×3.23』「え，ちがうよ，（82.8×3.23）×3.14だよ。かける順番を逆にしても結果は同じだけど，式としては間違いだよ。まぎらわしいんだよな，数値が。でも考え方は（82.8×3.23）×3.14だからね」

　高学年の小数の計算でも，かけ算の順序に注意して指導しているのかと思いながら，読み進めると，その直後に，後日談がカッコ書きとなっていました。

（後に気がついたことだが，直径が3倍になれば円周も3倍になると考えると両方とも同等に正しい。）

　冒頭の文章題に対して，82.8×3.14×3.23あるいは（82.8×3.14）×3.23の式もまた，正解になる，というわけです。
　ただし，「両方とも同等に正しい」であり，「どんな順番でもよい」と言っているわけではない点にも注意が必要です。3つの数の積で，どんな順番でもよいような事例として，直方体の体積（縦・横・高さ）が考えられますが，それとは状況が異なります。
　なぜ「どんな順番でもよい」ではないのかを考えるにあたり，正解となる（カッコを使用しない）2つの式は，ともに「82.8×」から始まっている点に注目したいところです．これは最終的に求めたい（円周の）円とは別の，円の直径です。かけ算の式を立てる際の，出発点となるのが，「82.8」だというわけです。
　次の文章題も，ここまで書いた性質を持っています。

5人家族があります。それぞれ，1日に3個ずつ，ミニトマトを食べます。7日間で，この家族は全部で何個のミニトマトを食べるでしょうか?

　解答は難しくありません。5人家族で1日に3個ずつ，ミニトマトを食べるというので，この家族が1日に食べるミニトマトは3×5＝15で15個です。7日間ですから，15×7＝105 答え105個となります。一つの式で表すと，3×5×7＝105です。
　別の考え方もできます。1日に3個ずつ，7日間ですから，1人が食べるミニトマトは3×7＝21で21個です。5人いますので，21×5＝35 答え105個となります。一つの式だと，3×7×5＝105です。
　この場合にも，式の最初の3であり，5や7にはなりません。この3は，「1人が1日に3個」，ミニトマトを食べるということと対応します。パー書きで表すと，「3個／人・日」です。https://www.nmij.jp/public/report/translation/IUPAC/より読むことのできる『物理化学で用いられる量・単位・記号 第3版』の表記を，個や人や日といった分離量の単位にも適用するなら，「」と表せます。ともあれ以下では「3個／人・日」をはじめ，パー書きを用います。
　3×5×7＝105という式に出現する，それぞれの数に，単位を付けると，「3個／人・日×5人×7日＝105個」となります。3×5＝15については，「3個／人・日×5人＝15個／日」で，5人家族で1日あたり15個食べる，と解釈できます。
　3×7×5＝105の式に対しては，「3個／人・日×7日×5人＝105個」であり，3×7＝21は「3個／人・日×7日＝21個／人」（7日間で1人あたり21個食べる）です。
　3×5×7のうちの5×7を，そして3×7×5のうちの7×5を，先に計算することも可能です。その積は，「35人・日」ですが，「35食」と読み替えることにします。1食で3個ずつ，ミニトマトを食べるとすると，35食分に必要なミニトマトの数は，「3個／食×35食＝105個」と表せます。
　ミニトマトの数については，1人が1日に食べる数を固定としたとき，人数と日数の両方に比例します。複比例です。その定数（複比例定数）は，1人が1日に食べる数であり，ここでは「3個／人・日」となるのでした。「人・日」を「食」に置き換えることで，「1あたり×いくつ分」が適用可能になった，というわけです。
　それでは，はじめに書いた，2つの円の問題では，求めるべき円周の長さは，もとの円の割合と，円周率の2つに比例すると言って，よいのでしょうか?
　2つ，難点があります。一つは「円周率に比例する」と言うと，まるで円周率が変量（説明変数）であるかのようですが，その解釈は自然でない*1こと，もう一つは，82.8×3.23×3.14における3.23×3.14や，82.8×3.14×3.23における3.14×3.23について，その積（形式的には10.1422で，無次元量です）に，「35人・日」または「35食」と同様の，量的な意味を与えるのが困難であることです．
　2つの文章題から考えることのできるかけ算の関係を，乗法的オペレータ*2に基づき，図にしてみます。ミニトマトの件は，以下のようになります。

　2つの円については，以下のとおりです。右上・左下・右下の計算結果（それぞれの長さ）は省略しています。もとの円の直径から，求めたい円周への矢印がないのは，先ほど書いた難点の2番目が理由となります。

　啓林館の算数6年の教科書にも，類題があり，さまざまな立式を含む授業例が報告されています。

• 防災計画（教科書教材） ( 小学校 ) - 授業がんばりＭＡＴＨ - Yahoo!ブログ

　画像より読むことのできる文章題は「たけしさんは7人家族です。災害に備えて，全員の3日分の水をそろえようと思います。1.5L入りのペットボトルを何本買うとよいでしょう。」です。そこに「1人1日に必要な水の量は3Lとします。」を付け加えれば，式を立てて計算し，「42本」という答えを得ることができます。
　2行3列で6個の式が，1つの画像になっています。総合式*3だと「3×7×3÷1.5」「3×3×7÷1.5」「3÷1.5×3×7」，分解式だと「3×7＝21　21×3＝63　63÷1.5＝42」「3×7÷1.5＝14　14×3＝42」「3×3÷1.5＝6　6×7＝42」です。いずれにおいても，最初の数は3で，「1人1日に必要な水の量は3L」に対応します。
　本文では「最初に7×3をして，「のべ21人分必要」ということから処理することもできるが子どもはしないでしょう。」がカッコ書きされています。「のべ」が時代を感じさせます。

　「ミニトマト」および「相似な図形の長さ」については，メインブログの記事もご覧ください。

• 3口のかけ算，かけ算の順序 - わさっき
• 相似な図形の長さ～新たな3口のかけ算 - わさっき

*1:「直径に円周率をかけると円周になる」と言うのは，差し支えありません。このことは「比例」と「かけ算」との違いとして，別の機会に再検討したいものです。

*2:http://www.shinko-keirin.co.jp/keirinkan/sansu/WebHelp/03/page3_12.html

*3:総合式と分解式の違いについては，例えばhttps://www.shinko-keirin.co.jp/keirinkan/sansu/WebHelp/03/page3_05.htmlで書かれています。『小学校学習指導要領解説算数編』には，「総合式」「分解式」のいずれの用語もない代わりに，第4学年で「四則を混合させたり（ ）を用いたりして一つの式に表すことには，数量の関係を簡潔に表すことができるなどのよさがあることが分かるようにし，四則を混合させたり（ ）を用いたりして一つの式に表すことができるようにすることが大切である。」と書かれており，総合式の意義は，その学年で学ぶべきとされています。