- 作者: 遠山啓
- 出版社/メーカー: 日本図書センター
- 発売日: 2012/02/29
- メディア: 大型本
- この商品を含むブログを見る
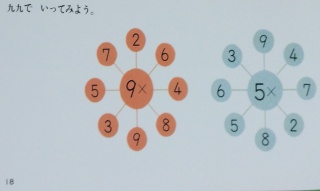
(p.18)真ん中の数を，周囲のそれぞれの数にかけて，素早く答えを言う練習問題です．例えば左側だと，「9×2＝18（くに18），9×6＝54（くろく54），…」などとなります．
この図式はこれまでにも見てきたのですが，ちょっとびっくりしたのは，中央が「9×」「5×」となっているところです．もちろん欧米式の「9倍」「5倍」を意味してはおらず，言葉にするなら「9かける」「5かける」，そして意味合いとしては，「9にまわりの数をかける」（5も同様）といったところでしょう．
記憶と記録をたどってみます．最初にこれを面白いと思ったのは，2012年6月のことで，もう一つのブログで記事にしています．
ここで最後に，図をお見せします．
他の本でも，目にしたことがあります．
筆算の順序 - わさっき
この問題を最初に見たときは，百ます計算の対抗くらいに思っていました．
しかし，筆算を念頭に置くと，また別の意義が浮かんできます．これは，中軸になる数を「かけられる数」，その外にある数を「かける数」として，いろいろな方向に「かける」ことができるようになってほしい，という出題意図になっています．筆算の素地指導なのです．
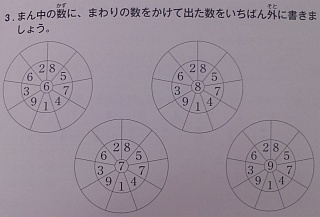
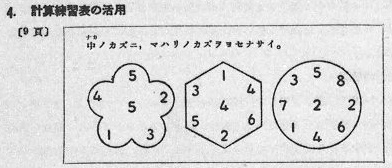
これと同様の図形を，戦前の書籍から見つけることができました．最初は，かけ算ではなくたし算です．
（高木佐加枝 (1935): 尋常小学算術書活用と補充 第1学年 下巻, p.65.）
「計算練習表」という名称がついています．http://kindai.ndl.go.jp/info:ndljp/pid/1457148とhttp://kindai.ndl.go.jp/info:ndljp/pid/1462874*1を読み直したところ，たし算，ひき算，かけ算の，いろいろな計算問題で出現します．
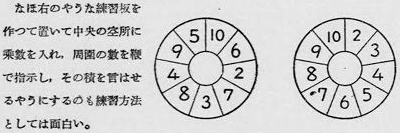
かけ算の問題の初出は次のとおりです．「中央の空所に乗数を入れ」となっており，もともと中央は，かける数でした．
（高木佐加枝 (1936): 尋常小学算術書活用と補充 第2学年 上巻, p.289）
内容は割愛しますが，『算数に強くなる水道方式入門 (1961年)』p.207にも4つ，真ん中の数を，周囲のそれぞれの数にかけるという出題があります．中央は「7×」などとなっています．
