乗法が用いられる具体的な場面を，×の記号を用いた式に表したり，その式を具体的な場面に即して読み取ったり，式を読み取って図や具体物を用いて表したりすることを重視する必要がある。
『小学校学習指導要領（平成29年告示）解説算数編』，p.155の記述です。対応する，（解説のつかない）学習指導要領の事項は，「乗法が用いられる場面を式に表したり，式を読み取ったりすること。」です。
引用した文について，「たり」に着目すると，以下の3つの活動を取り出すことができます。
- 具体的な場面を，×の記号を用いた式に表す。
- 式を具体的な場面に即して読み取る。
- 式を読み取って図や具体物を用いて表す。
この3つは，活動のインプットとアウトプットがそれぞれ異なります。最初の「具体的な場面を，×の記号を用いた式に表す」について，インプットとしては「文章題」が典型的ですが，「図」となることもあります。アウトプットは「×の記号を用いた式」で，端的にいうと「式」です。
一つ飛ばして，「式を読み取って図や具体物を用いて表す」の，インプットは，4×3といった「式」です。アウトプットは，「図」や「具体物」です。図でよく見かけるのは，○の並びです。具体物としては，おはじきなどがあります。
あいだの「式を具体的な場面に即して読み取る」について，インプットは「式」だけではありません。「具体的な場面」も，インプットに含まれます。「読み取る」活動のアウトプットは，式に出現する数，そして式全体が何を表すかを，文にすることです。令和2年度全国学力・学習状況調査の算数の「求め方の中の「5×4」は，どのようなことを表していますか。」の出題が当てはまります*1。「5×4」という式だけを見ても，正解を得ることができず，求め方の文と，それより上の説明文や図の内容を取捨選択して，答えを作る必要があったのでした。
「式を具体的な場面に即して読み取る」には，インプットは上記と同じで，アウトプットが異なる活動があることに，気づきました。アウトプットは，煎じ詰めれば「真偽値」です。「式」が，「具体的な場面」を表しているのなら，Trueを返し，そうでなければ，Flaseを返すのです。この読み取り活動は，真偽判定ということもできます。小学校の算数では，TrueとFalseはそれぞれ，「正しい」と「まちがい」に置き換えることになります。なお，ここまでの内容は，https://twitter.com/takehikom/status/1560837169971097600（現在は読めません）から始まる一連のツイートを，ブログ用に書き直したものです。
先日購入した書籍で，この真偽判定を含む指導事例を見かけました。
3年「わり算」の「実際の指導事例」です(pp.32-33)。四角で囲まれた文章題は，「クッキーが12こあります。1人に4こずつ分けると，何人に分けられますか。」です。それより前の文章に書かれているとおり，「包含除」の場面です。「等分除」は学習済みで，包含除はこの授業が初めてです。
この文章題を，数ブロックや図を使って説明するとなったときに，「あれっ? なんだかおかしいな。」と言い出す児童がいます。教師が指名して，黒板を使って操作させると，等分除に対するトランプ配りです*2。他の児童に問うと，「4個ずつ分けて，答えが3人とわかる問題。」ということで，以下の操作を行います。
そのあと教師と児童とのやり取りを見ると，かけ算の式の真偽判定が行われています。少し長くなりますが書き出します(p.33)。
T*3：これは，何人に分けられるかを求めるわり算で，式は12÷4＝3です。わり算は，かけ算で表せました。□を使った式をノートに書きましょう。
C：4×□＝12
C：□×4＝12
T：（子どものノートにあった式を板書して）式が2つありました。どちらが正しいと思いますか? 4×□＝12と思う人はグー，□×4＝12たと思う人はチョキをだします。せーの，どっち!
T：どうして，そう思ったの?
C：□×4＝12だったら，「□人のまとまりが4個のあめ分で，全部で12個のあめがある」という意味でよくわからない。
C：□×4＝12だったら，□は人だから，12の単位が「人」になって変。
C：4×□＝12は，4個のあめのまとまりが幾つ分あるかだから正しい。
「クッキーが12こあります。1人に4こずつ...」の文章題や図を「具体的な場面」とし，それと「□×4＝12」という「式」との組み合わせだとFalseとなるのを，終わりから3番目と2番目の児童が別々の理由をつけて発表し，式が「4×□＝12」のときにはTrueとなるのを，最後の児童が理由をつけて発表しています。
□がかけられる数に来るときが等分除で，かける数に来るときが包含除となるのは，この本のオリジナルというわけではなく，『小学校学習指導要領（平成29年告示）解説算数編』p.148に「等分除は，□×3＝12の□を求める場合であり，包含除は3×□＝12の□を求める場合である。」という文があるほか，算数授業研究135号 p.29に書かれているのは「包含除（a×□＝c）」「等分除（□×b＝c）」です。Greer (1992)は，"3 children have 4 cookies each."を「子どもが最初にかけ算を用いる場面」とした上で，子どもの数が「かける数(multiplier)」，クッキーの数(4 cookies)が「かけられる数(multiplicand)」に対応すること，そして2種類のわり算を考えることができてそれぞれ区別されることを，指摘しています。
*1:https://takexikom.hatenadiary.jp/entry/2021/01/29/055223
*2:「操作1」の図もあります。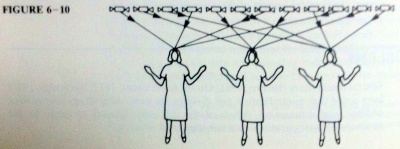
や，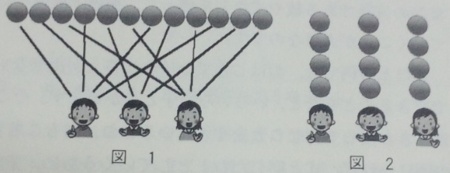
の図1と（個数も分ける人数も）同じです。
*3:ここの説明と指示には，違和感があります。等分除のみを学習した段階では，除法と乗法との関係は12÷4＝□⇔□×4＝12と表せます。そして，12÷4＝□⇔4×□＝12という関係は未習の状態で，「□を使った（かけ算の）式をノートに書」かせているように見えるのです。
