ある種の「かける順序を問わない場面」について整理します。小学校の算数で出題したとき,式は,a×b×cでもa×c×bでもかまいませんが,aが乗算記号の右に来ることは,期待されていません。
はじめに考える文章題は,以下のものです。「相似な図形の長さ」の応用題です。
82.8cmの直径の円があります。その3.23倍の直径の円の円周は何cmでしょうか。
円周率は3.14とします。答えとなる長さだけでなく,式も書くこととします。
素朴な求め方は,こうです。円周を求めたい円の直径は,82.8cmの3.23倍ですから,82.8×3.23で求められます。そして円周=直径×円周率を使えば,円周は82.8×3.23×3.14と表せます。
電卓で計算してみますと,839.77416となりました。答えは839.77416cmです。小数点以下が細かすぎるようにも見えますが,1桁たりともおろそかにしないという方針のもと,計算させるのは差し支えないでしょう。
別の考え方もできます。82.8cmの直径の円について,先に,円周の長さを式にします。8.28×3.14です。そして,直径が2倍,3倍,…になると円周の長さも2倍,3倍,…になりますので,求めたい長さは82.8×3.14×3.23となります。計算結果(839.77416)は変わりません。
この文章題は,以下の文献で取り上げられています。「教授学の探究」は大学の紀要と思われますが,著者は小学校教師です。
- 佐藤敬行, 問題づくりを通して乗除演算の意味を考える―「いろいろな文章問題」(小学校5年)の実践から, 教授学の探究, 北海道大学大学院教育学研究科教育方法学研究室, Vol.23, pp.27-54 (2006). http://ci.nii.ac.jp/naid/120000964041 http://hdl.handle.net/2115/13659
本文に,授業中のやりとりも載っています(pp.31-32)。「 」が先生,『 』が子どもの発言として読めば,話が合います。
「(2)の式は?」『82.8×3.14×3.23』「え,ちがうよ,(82.8×3.23)×3.14だよ。かける順番を逆にしても結果は同じだけど,式としては間違いだよ。まぎらわしいんだよな,数値が。でも考え方は(82.8×3.23)×3.14だからね」
高学年の小数の計算でも,かけ算の順序に注意して指導しているのかと思いながら,読み進めると,その直後に,後日談がカッコ書きとなっていました。
(後に気がついたことだが,直径が3倍になれば円周も3倍になると考えると両方とも同等に正しい。)
冒頭の文章題に対して,82.8×3.14×3.23あるいは(82.8×3.14)×3.23の式もまた,正解になる,というわけです。
ただし,「両方とも同等に正しい」であり,「どんな順番でもよい」と言っているわけではない点にも注意が必要です。3つの数の積で,どんな順番でもよいような事例として,直方体の体積(縦・横・高さ)が考えられますが,それとは状況が異なります。
なぜ「どんな順番でもよい」ではないのかを考えるにあたり,正解となる(カッコを使用しない)2つの式は,ともに「82.8×」から始まっている点に注目したいところです.これは最終的に求めたい(円周の)円とは別の,円の直径です。かけ算の式を立てる際の,出発点となるのが,「82.8」だというわけです。
次の文章題も,ここまで書いた性質を持っています。
5人家族があります。それぞれ,1日に3個ずつ,ミニトマトを食べます。7日間で,この家族は全部で何個のミニトマトを食べるでしょうか?
解答は難しくありません。5人家族で1日に3個ずつ,ミニトマトを食べるというので,この家族が1日に食べるミニトマトは3×5=15で15個です。7日間ですから,15×7=105 答え105個となります。一つの式で表すと,3×5×7=105です。
別の考え方もできます。1日に3個ずつ,7日間ですから,1人が食べるミニトマトは3×7=21で21個です。5人いますので,21×5=35 答え105個となります。一つの式だと,3×7×5=105です。
この場合にも,式の最初の3であり,5や7にはなりません。この3は,「1人が1日に3個」,ミニトマトを食べるということと対応します。パー書きで表すと,「3個/人・日」です。https://www.nmij.jp/public/report/translation/IUPAC/より読むことのできる『物理化学で用いられる量・単位・記号 第3版』の表記を,個や人や日といった分離量の単位にも適用するなら,「」と表せます。ともあれ以下では「3個/人・日」をはじめ,パー書きを用います。
3×5×7=105という式に出現する,それぞれの数に,単位を付けると,「3個/人・日×5人×7日=105個」となります。3×5=15については,「3個/人・日×5人=15個/日」で,5人家族で1日あたり15個食べる,と解釈できます。
3×7×5=105の式に対しては,「3個/人・日×7日×5人=105個」であり,3×7=21は「3個/人・日×7日=21個/人」(7日間で1人あたり21個食べる)です。
3×5×7のうちの5×7を,そして3×7×5のうちの7×5を,先に計算することも可能です。その積は,「35人・日」ですが,「35食」と読み替えることにします。1食で3個ずつ,ミニトマトを食べるとすると,35食分に必要なミニトマトの数は,「3個/食×35食=105個」と表せます。
ミニトマトの数については,1人が1日に食べる数を固定としたとき,人数と日数の両方に比例します。複比例です。その定数(複比例定数)は,1人が1日に食べる数であり,ここでは「3個/人・日」となるのでした。「人・日」を「食」に置き換えることで,「1あたり×いくつ分」が適用可能になった,というわけです。
それでは,はじめに書いた,2つの円の問題では,求めるべき円周の長さは,もとの円の割合と,円周率の2つに比例すると言って,よいのでしょうか?
2つ,難点があります。一つは「円周率に比例する」と言うと,まるで円周率が変量(説明変数)であるかのようですが,その解釈は自然でない*1こと,もう一つは,82.8×3.23×3.14における3.23×3.14や,82.8×3.14×3.23における3.14×3.23について,その積(形式的には10.1422で,無次元量です)に,「35人・日」または「35食」と同様の,量的な意味を与えるのが困難であることです.
2つの文章題から考えることのできるかけ算の関係を,乗法的オペレータ*2に基づき,図にしてみます。ミニトマトの件は,以下のようになります。
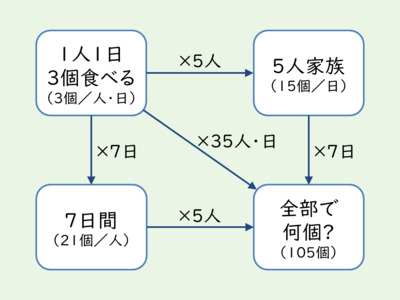
2つの円については,以下のとおりです。右上・左下・右下の計算結果(それぞれの長さ)は省略しています。もとの円の直径から,求めたい円周への矢印がないのは,先ほど書いた難点の2番目が理由となります。
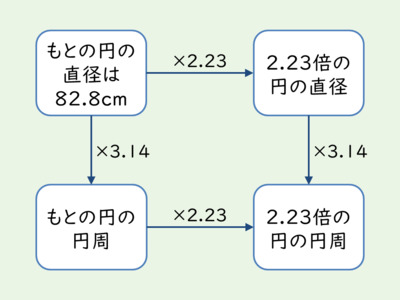
啓林館の算数6年の教科書にも,類題があり,さまざまな立式を含む授業例が報告されています。
画像より読むことのできる文章題は「たけしさんは7人家族です。災害に備えて,全員の3日分の水をそろえようと思います。1.5L入りのペットボトルを何本買うとよいでしょう。」です。そこに「1人1日に必要な水の量は3Lとします。」を付け加えれば,式を立てて計算し,「42本」という答えを得ることができます。
2行3列で6個の式が,1つの画像になっています。総合式*3だと「3×7×3÷1.5」「3×3×7÷1.5」「3÷1.5×3×7」,分解式だと「3×7=21 21×3=63 63÷1.5=42」「3×7÷1.5=14 14×3=42」「3×3÷1.5=6 6×7=42」です。いずれにおいても,最初の数は3で,「1人1日に必要な水の量は3L」に対応します。
本文では「最初に7×3をして,「のべ21人分必要」ということから処理することもできるが子どもはしないでしょう。」がカッコ書きされています。「のべ」が時代を感じさせます。
「ミニトマト」および「相似な図形の長さ」については,メインブログの記事もご覧ください。
*1:「直径に円周率をかけると円周になる」と言うのは,差し支えありません。このことは「比例」と「かけ算」との違いとして,別の機会に再検討したいものです。
*2:http://www.shinko-keirin.co.jp/keirinkan/sansu/WebHelp/03/page3_12.html
*3:総合式と分解式の違いについては,例えばhttps://www.shinko-keirin.co.jp/keirinkan/sansu/WebHelp/03/page3_05.htmlで書かれています。『小学校学習指導要領解説算数編』には,「総合式」「分解式」のいずれの用語もない代わりに,第4学年で「四則を混合させたり( )を用いたりして一つの式に表すことには,数量の関係を簡潔に表すことができるなどのよさがあることが分かるようにし,四則を混合させたり( )を用いたりして一つの式に表すことができるようにすることが大切である。」と書かれており,総合式の意義は,その学年で学ぶべきとされています。







