ツイッターを中心に見かける,いわゆる「かけ算の順序論争」を,国内外の学術文献や授業事例(批判も)に注意しながら,簡潔に表すなら,「掛算順序強制vs乗法意味理解」となります。
「掛算」で連想するのは,ハッシュタグ「#掛算」です。それに対し「乗法」の語が,小学校学習指導要領の算数では使用されています。小学校での学習(導入)は第2学年ですが,第4学年の「乗数や除数が整数である場合の小数の乗法及び除法の計算の仕方を考え,それらの計算ができること。」は,連続量×分離量と書くこともでき,さらに上の学年の,小数どうし,分数どうしの乗除算の基礎となります。
「順序強制」と「意味理解」に関しては,それぞれの特徴がよく現れた文献を一つずつ,挙げることにします。
なお,[黒木2014]が収録された「季刊理科の探検 2014秋号」は,Kindleでも読むことができます。[布川2010]は,リンク先より(アクセスするとURLが変わります),誰でも無料でダウンロードできます。
それぞれの文献において,注目すべき記載内容を,メインブログ・本ブログで以前に取りまとめた記事より転載します。
現代の算数教育の世界には次のようなドグマ(教義)があるようだ。
- 文章や絵で示された具体的場面を式だけで忠実に表現できるし、しなければいけない。逆に式だけから具体的場面を一意的に読み取れる。
- 「2×8」のような式だけを見て、子どもの理解度を測ることができる。
([黒木2014, p.114],転載元)
2年生の導入時では,被乗数と乗数を明確に区別して扱っているが,これもかけ算の意味の理解を確かにするためと考えられる.図1のみかん全部の個数を4×6=24と表すときに,被乗数4が一つ分の大きさ,乗数6が幾つ分を表していることを大切に扱う必要がある.ただしこの意味は世界共通でなく,例えば英語ではこれを6×4=24とするので,被乗数,乗数の意味は逆になる.なお昭和44年の「小学校指導書算数編」では,基準にする大きさのいくつ分かにあたる大きさを「表わす」ことに触れているが,表現という側面からは被乗数と乗数の意味が特に重要となる.またかけ算の学習は,例えば2の段では被乗数が2の場合に乗数を1から9まで系統的に変化させ(図2),8×2などはここで扱わないが,これもかけ算の意味を大切にしていることの一つの現れであろう.
([布川2010, p.50],転載元)
個人的には[布川2010]の記載内容や,現在の小学校学習指導要領・同解説の算数の記載,そして小学校の授業を通じてなされている活動に賛同します。把握する限り,[黒木2014]の上記引用を支持する国内外の学術文献は見出せず,控えめに言って,当該著者の独自見解です。これを読むより前に,メインブログで取りまとめたQ&Aで「歯切れがよくて威勢がいいものだから,閉塞感のある時代においてはブームになる危険性を持ち,それに迎合する人々が現れるのが恐いところです.加えて,主張はそれなりに明快なのですが,それを実現させるための具体的・現実的な論考が全く無いのも特徴です.」*1と書いたのですが,[黒木2014]の内容全体に当てはまるものとなっています。
ここで,批判者から学習者にスイッチ*2します。[布川2010]の「かけ算の意味」や,「2の段では被乗数が2の場合に乗数を1から9まで系統的に変化させ」に,関係しそうな英語の論文を最近,入手して読みました。
タイトルを日本語に訳すと「かけ算に関する教科書の分析―日本,シンガポール,タイの事例」といったところでしょうか。著者はともにタイの研究者です。TIMSS(国際数学・理科教育調査)で日本とシンガポールは非常に良い成績をあげており,その理由を,タイを入れた3か国の教科書に求めようという内容です。
全体をざっと読んでから,REFERENCES(参考文献)を注意深く見ました。この論文では,日本の算数の教科書として,学校図書の2005年(平成17年)発行のものを参照しており,「Tosho, G. (2005). Mathematics for elementary school for first grade. Tokyo: Gakkoh Tosho Co., Ltd.」が入っています(まるで「学校」がファーストネーム,「図書」がファミリーネームのようです)。「Isoda, M. (2010).」の文献は小学校学習指導要領解説算数編の日英対訳です.「Fujii, T. (2001).」のURLはデッドリンクとなっていました。
本文で,対象とした日本の教科書の特徴がもっともよく現れているのは,p.260右カラムの一つの段落です。訳してみました。
In the Japanese second grade textbooks, the sequences of topics in multiplication are: learning unit 1; the meaning of multiplication, multiplication sentence, unit 2: the multiplication tables of 2, 5, 3, 4, unit 3: multiplication tables of 6, 7, 8, 9, 1, and unit 4: multiplication table, multiplication game. In summary, the learning units of multiplication are organized as the meaning of multiplication, multiplicands, multipliers, and multiplication table. The laws of calculation (commutative, associative, and distributive), algorithm and the rules of multiplication are introduced in the elementary mathematics textbooks.
(日本の2年の教科書では,かけ算のトピックの順番は次のようになっている。単元1は,かけ算の意味およびかけ算の式,単元2は,2の段,5の段,3の段,4の段のかけ算,単元3は,6の段,7の段,8の段,9の段,1の段のかけ算,そして単元4は,九九の表やかけ算あそびである。要約すると,かけ算学習の単元は,「かけ算の意味」「かけられる数」「かける数」「九九の表」として系統化されている。かけ算に関する計算の法則(交換法則,結合法則,分配法則)や,アルゴリズムおよびルールも,小学校の算数の教科書で紹介されている.)
「かけ算の意味(the meaning of multiplication)」「かけられる数(被乗数,multiplicand)」「かける数(乗数,multiplier)」は,[布川2010]と[Boonlerts 2013]とで共通して出現する,教科書の特徴と言っていいでしょう。なお,[布川2010]では参考文献に,学校図書の教科書を挙げているほか,平成27年度用の学校図書の算数教科書の著作者に,「布川 和彦」の名前を見つけることができます。
ただし2つの文献間で,引用・被引用は見られません。同一の情報源について,異なる立場からその特徴が書かれており,おおむね一致しているものと判断できます。
[Boonlerts 2013]は,また別の情報源と照合することもできます。本文で「Greer (1992)」と書き,引用している文献です。かけ算の学習におけるtypes of multiplication(乗法が用いられる場合)として,日本の教科書は「equal group(同等のグループ)」「rectangular array(2次元アレイ)*3」「multiplicative comparison(乗法的な比較)」の3つが使用されているのに対し,シンガポールは「同等のグループ」「2次元アレイ」の2つ,そしてタイは「同等のグループ」のみだというのです。
同等のグループは,小学校学習指導要領解説算数編に書かれた「乗法は,一つ分の大きさが決まっているときに,その幾つ分かに当たる大きさを求める場合に用いられる。」と結びつけることができます。アレイについてはアレイ図 (2015.12) - わさっきで整理しています。乗法的な比較は,倍概念のことと思われます。
本記事は,「順序の強制」と「意味の理解」のどちらが,算数教育・初等教育の実態を表しているかについて,答えを与えるものではありません。しかしながら,関連情報の充実度合いや,教材研究・授業研究への支援という観点では,後者というほかありません。
(翌日追記)[黒木2014]より引用した中の「式だけから具体的場面を一意的に読み取れる」について,反例となるような授業案があるのを,思い出しました。
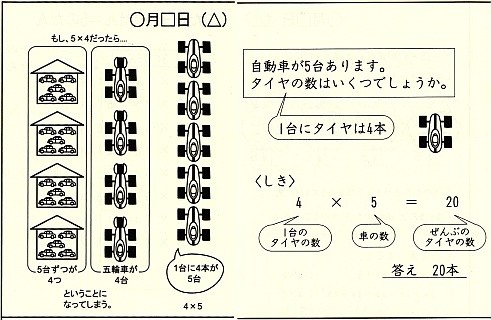
この図は『板書で見る全単元・全時間の授業のすべて 小学校算数2年〈下〉』のpp.46-47によるもので*4,『新版 小学校算数 板書で見る全単元・全時間の授業のすべて 2年下』のpp.44-45にも同様の図があります。上下の横線が真ん中付近で切れているのは,そこがページの切れ目でして,さらに右には式が並んでおり,一つの板書例という見せ方になっています。
かけ算の順序論争について(日本語版) - わさっきの記述を書き直す形で,画像の見方を説明します。「自動車が5台あります。タイヤの数はいくつでしょうか」という問題から始まります。「1台にタイヤは4本」を,クラス内で共有*5したのち,正解となる式は「4×5=20」です。
ここでもし,「5×4」だったら,5つのタイヤがついて「五輪車が4台」となる図や,家に車が入った「5台ずつが4つ」という図が現れます(板書は容易ではなく,先生が紙に書くなどして用意しておく必要があるでしょう)。いずれも,問題に合っていません。
これらは異なる具体的場面であるとともに,他のかけ算の文章題にも適用できます。例えば「さらが 5まい あります。1さらに りんごが 3こずつ のって います。りんごは ぜんぶで 何こ あるでしょう。」に対して「5×3=15」としたら,「5個ずつ3皿」や「5枚×3で15枚になる」といった読み取り方を,挙げることができるのです。
なお,「五輪車が4台」と同様の解釈については,朝日新聞の2×8ならタコ2本足 - 花まる先生公開授業が知られていますが,他書では『アイディアシートでうまくいく! 算数科問題解決授業スタンダード』にも見ることができます*6。「5台ずつが4つ」については,1951年のhttps://erid.nier.go.jp/files/COFS/s26em/chap5.htmにおける「3は人数を表わしている数である。それを2倍した答の6は何といったらよいか尋ねてみる。それで,6人となって問題の要求に合わないことを説明する。」のところや,Vergnaud (1988)の"Twenty dollars cannot be 5 cars + 5 cars + 5 cars + 5 cars."の文*7も同じ趣旨と言えます。
タイヤの数を求める問題については,[布川2010]の,次の記述も関連すると言っていいでしょう:「(略*8)一つ分が明示的でない場合に,自分で一つ分を設定し,場面を(一つ分の大きさ)×(幾つ分)として構造化し,表現することを経験するもので,わが国での意味の重視にそった活動と言える.また,1年生で○こずつを探す(三輪車のタイヤは3つずつ等)活動があるが,これも一つ分を自分で設定することの素地的な経験となっている.」













