『小学校学習指導要領(平成29年告示)解説算数編』の記載の中で,「式の意味」を,図や言葉と関連付けて使用している箇所があります(p.270)。
文科省サイトで確認するなら,https://www.mext.go.jp/component/a_menu/education/micro_detail/__icsFiles/afieldfile/2019/03/18/1387017_004.pdf#page=276です。文章は「このように,図で表した関係を式にしたり,式に表した関係を図で表したり,図や式の意味を言葉で説明したりすることが大切である。」で締めくくられています。
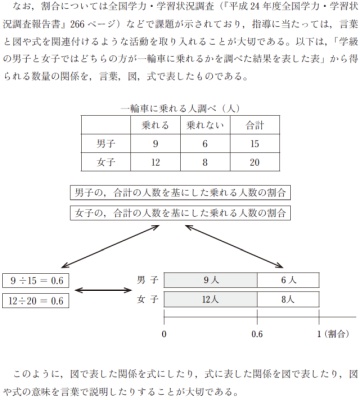
上で画像として貼り付けた内容から読み取れるのは,次のことです。「一輪車に乗れる人」を,学級の男女に分けて調べて,表にしたところ,男子の「乗れる」は9人,「乗れない」は6人でした(合計15人*1)。それに対し女子の「乗れる」は12人,「乗れない」は8人でした(合計20人)。
この集計結果をもとに,「学級の男子と女子ではどちらの方が一輪車に乗れるか」を考えます。「乗れる」の列の大小関係から,女子の方が多いじゃないかという推論は(結論としては),ここでは期待されません。
「どれだけ『乗れる』か」を数値化するため,男女それぞれで,「合計の人数を基にした乗れる人数の割合」を計算します。男子は「9÷15=0.6」です。それに対し女子は「12÷20=0.6」です。式の右には,男女それぞれの割合に関するテープ図が描かれています。
結果として,この表からは,「合計の人数を基にした乗れる人数の割合」が男女で同じ0.6となり,「どちらが」への答えは,「どちらも同じ割合」となります。
ここまでについて,割合の意味として,「割合=比べる量÷もとにする量」を活用しています。注意したいのは,「割合=比べる量÷もとにする量」は,割合の定義ではない点です。https://www.shinko-keirin.co.jp/keirinkan/sansu/WebHelp/05/page5_21.htmlによると,「割合は,2つの量を比べるときに用いられるもので,ある量をもとにして,他方の量がその何倍にあたるかを表した数です。」とあり,これが割合の定義*2です。「割合=比べる量÷もとにする量」は,「もとにする量の何倍になっているか」を,「わり算」で求めるための手段となります。
次に,式の意味としては,「9÷15=0.6」のほうが,「男子の,合計の人数を基にした乗れる人数の割合」を表した式となります。ここにも注意書きを加えると,この等式の9が「比べる量」,15が「もとにする量」にそれぞれ対応しますが,「0.6」は割合の言葉の式の「割合」に,直結しません。言葉を交えて式にするなら,「男子の,合計の人数を基にした乗れる人数の割合=男子の,乗れる人数÷男子の,合計人数=9÷15=0.6」であり,この両端を見ることで,「男子の,合計の人数を基にした乗れる人数の割合は,0.6だ」というわけです。
「12÷20=0.6」についても同様に,この式の意味は,「女子の,合計の人数を基にした乗れる人数の割合」です。それぞれの式に「男子の…割合」「女子の…割合」を対応付けることを,このページでは「式の意味を言葉で説明」と書いていますが,(解説のつかない)小学校学習指導要領の表記のうち「式の意味を読み取ったりすること」も該当します。
「ある量をもとにして,他方の量がその何倍にあたるかを表した数」で定義される,割合は,男子も女子も0.6で「同じ」だけれど,求める式は「9÷15=0.6」と「12÷20=0.6」のように「違う」のであり,9と15,12と20のそれぞれに「意味がある」と言うこともできます。
さて,この一輪車の件で,割合を求める式は「9÷15=0.6」「12÷20=0.6」の2つだけでしょうか?
そうではないよ,「基準量(もとにする量)」・「比較量(比べる量)」として適切なものを選んで,割合を求める必要があるのだよというのが,「平成24年度全国学力・学習状況調査報告書」で書かれています。全国学力・学習状況調査を起点に,問題文と解説は,それぞれ以下より見ることができます。小学校算数B 大問5 (3)です。
- https://www.nier.go.jp/12chousa/12mondai_shou_sansuu_b.pdf#page=20
- https://www.nier.go.jp/12chousakekkahoukoku/03shou-gaiyou/24_shou_houkokusyo-4_sansuub.pdf#page=44
「男子と女子それぞれで,合計の人数をもとにした乗れる人数の割合を比べます。男子と女子ではどちらのほうの割合が大きいですか。」という出題で,正解は「3 男子と女子の乗れる人数の割合は同じ。」です。また「その番号を選んだわけを,言葉や式を使って書きましょう。」とも問うており,解答類型・反応率の表に書かれた正答例は,「男子の乗れる人数の割合は,9÷15で,0.6です。女子の乗れる人数の割合は,12÷20で,0.6です。だから,男子と女子の乗れる人数の割合は,0.6で同じです。」となっています。
解説を読んでいくと,「9÷6=1.5」という式も出てきます。「式の意味を考えることにより,この式は「乗れない人数を基にした乗れる人数の割合」であることを言葉や図によって確認することができる。」と続いています。「9÷6=1.5」という式でも,「割合」を求めることはできる(これは何の割合であるかを説明できる)けれども,「合計の人数をもとにした乗れる人数の割合」ではない,というわけです。
さまざまな情報源を組み合わせて真相に迫ることを,これからも当ブログでは実施していきます。