若手教師のための算数指導66の教養 (算数科授業サポートBOOKS)
- 作者:飯田 慎司
- 発売日: 2020/12/23
- メディア: 単行本
書店で購入しました。Amazonでは,発売日は「2020/12/23」とのことですが,書籍の奥付では「2021年1月初版第1刷刊」と書かれていました。
各項目が見開きで,解説されています。通して読んだところ,「「被乗数と乗数」や「被除数と除数」という認識」(pp.80-81)というのがありました。4年の一項目としつつも,内容の大部分は5年(小数×小数)です。「被乗数と乗数をともに10倍した19×24の計算をして100でわる」(p.81)については,当ブログで今年,×10,×10,そして100でわるという記事を公開していました。
かけ算について,一読しただけでは分からなかった箇所を取り上げます(p.39)。
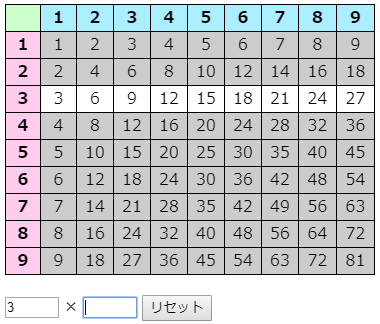
以下は,3の段の九九を例にして,乗法と除法の関係を指摘したものです。
かけ算九九の原理を,5年で学習する□と△を使って表すと,3の段は,3×□=△となります。このことをもとにして,3年で学習するわり算をかけ算の逆演算として考察すると,△÷3=□という包含除が対応してきます。「12個のリンゴを3個ずつに皿にのせると,皿はいくつできますか」という問題がその一例です。一方,等分除に当たるわり算は,□×3=△というかけ算の逆演算であり,「12個のりんごを3人で同じ数に分けると,1人何個ずつに分けられますか」という問題がその一例になります。このような考察からわかるのは,かけ算九九の意味から直接的につながるわり算は,等分除ではなく包含除だということです。
「乗法と除法の関係*1」「包含除」「等分除」は,個人的な理解と合致しています*2。後二者についてはメインブログで整理してきました。
不可解だったのは,最後の文の「このような考察からわかるのは,かけ算九九の意味から直接的につながるわり算は,等分除ではなく包含除だということです。」です。
九九の表を思い浮かべて,積(表内の値)と,因数の一つ(表側または表頭*3の値)を指定すると,もう一つの因数(表頭または表側の値)が一意に定まる,というのが,九九表から得られる,乗法と除法の関係であり,そこに等分除や包含除を持ち込むべきではないと,何度か読んで思案しました。
九九と包含除とを結び付ける記述は,あとのp.45でも見ることができました。
(略)日常生活では等分除を必要とする場合が多く,先に指導するのが一般的です。しかしながら,包含除を軽視することは不適切です。「4×□=△」という4の段のかけ算九九の逆演算としてのわり算は包含除であり(略)
この中の「4の段のかけ算の九九」と,p.39に戻って「3の段の九九を例にして」を合わせることで,著者の見方が推測できました。表に基づいて説明すると,九九は一つの表としてあらわされますが,「○の段」としたときには,表の特定の行だけを見ることになります。
メインブログの中に,「3の段」の画像例がありました。
算数の教科書や書籍で見かける九九の表は,各行を被乗数(○の段)とし,表側には「かけられる数」を並べます。そして各列が乗数で,表頭には「かける数」です*4。
そうしたとき,表内の値と,それと同じ行になる表側の値を指定すると,表頭の値が求められる(一意に定まる)のが,九九の表を用いた包含除と言えます。表側・表頭を入れ替えると,等分除となります。
先に述べた,「積(表内の値)と,因数の一つ(表側または表頭の値)を指定すると,もう一つの因数(表頭または表側の値)が一意に定まる」は,因数×因数=積に基づくかけ算とわり算の関係といえます。
九九の表を考えるときに,○の段,したがって行を強く意識することは,数学の行列の扱いが関連してきます。当ブログを開設した年に,メインブログで,文章を書いていました。
それでもなお,プログラミングを学習する人が,数学の行列を理解する理由,というよりは「これだけは理解してほしい」という点を挙げるなら,行と列の非対称性だと思っています.
数学的には,ある与えられた行列から,特定の行や列を抜き出したり,特定の行や列に関する演算をする際に,行と列とで,コスト面での違いは見られません.しかしプログラムを書くと,違ってきます.素直なコーディングでは,行のコピーはmemcpyでできても,列のコピーはそうはいかず,forループを用いた鈍くさい方法をとらざるを得ません.
*1:念のため,解説のつかない小学校学習指導要領の算数を確認しておくと,第3学年の「A 数と計算」の(4)(ウ)には,「除法と乗法や減法との関係について理解すること。」と記されています。
*2:と思ったのですが,びっくりした記述が入っていました。引用の中の「△÷3=□という包含除が対応してきます」について,「△÷3=□」という式は,等分除でも,包含除でも使用される式です。包含除を端的に表した式は,3×□=△のほうです。
*3:表側・表頭は,統計の表に関する用語です。https://www.intage.co.jp/glossary/403/, https://www.stat.go.jp/koukou/howto/process/newproc3_3.htmlなど
*4:リーグ表(対戦表)との関連を,http://takexikom.hatenadiary.jp/entry/2018/04/20/051229の脚注に書いていました