— takehikom (@takehikom) March 7, 2018
サミュエル・ジョンソンの「愛国心とは、ならず者たちの最後の避難所である」*1を改変したもので，内容面では，RikaTan（理科の探検） 2018年4月号*2に掲載された「「かけ算には順序がある」と教える教師たち 正解が×にされる不条理」を念頭に置いたものです。
「掛（か）け算の順序」に相対するのは，「乗法（かけ算）の意味」であり，「学習者の道を選ぶこと」です。
（公開：2022-01-18 早朝）
円の円周を，円周率を使った式で表す
- 山本弘: 「かけ算には順序がある」と教える教師たち 正解が×にされる不条理, RikaTan（理科の探検） 2018年4月号（通巻31号）, pp.36-39 (2018).
Kindle版を購入しました。通して読んで，文句しか付けようのない内容でした。
全体を通して，情報源が古いのです。RikaTanでは2014年に異なる著者による特別寄稿が掲載されている*1のに，それと今回とで何が違うのか，その間にどのような変化があったのかが，一切記されていません。「その間に」で思い浮かぶのは，昨年公表された，学習指導要領およびその解説なのですが，言及なしです。「現在の学習指導要領では、かけ算の順序に関して特に規定されていない」(p.36)については，小数×整数は4年で，小数×小数は5年で学習することと，整合性がとれません。
![RikaTan（理科の探検） 2018年4月号 [雑誌] Rikatan(理科の探検)](https://images-fe.ssl-images-amazon.com/images/I/61Q-2dRtXAL._SL160_.jpg "RikaTan（理科の探検） 2018年4月号 [雑誌] Rikatan(理科の探検)")
RikaTan（理科の探検） 2018年4月号 [雑誌] Rikatan(理科の探検)
- 出版社/メーカー: 文理
- 発売日: 2018/02/26
- メディア: Kindle版
- この商品を含むブログを見る
教師とのやりとりが，pp.37-38に見られます。
公式を書いたら×にされる?
少し前、ニセ科学関連の講演をやったとき、かけ算順序固定を子供に教えている小学校教師に会った。僕が講演の中で順序固定を批判したのがお気に召さなかったらしく、順序固定のメリットを力説する。あいにく、どれもみんな僕の知っていることばかりだったが。
僕はその際、以前から気になっていた質問をしてみた。
「たとえば『半径3cmの円の円周の長さを求めなさい』という問題の場合、どういう式を書くんですか?」
するとその教師、「待ってました」と言わんばかりの嬉しそうな表情を浮かべ、ホワイトボードに式や図を描いて自信たっぷりに説明しはじめた---円の面積の求め方を。
円の面積を求める方法は、説明するのは難しい。おそらくこの教師も、しょっちゅう子供がひっかかってしまうことに手を焼き、説明のしかたをマニュアル化して頭に叩きこんでいたのだろう。そのため、僕が「円の円周を求める問題」と言ったとたん、「いつもの問題だ!」と早とちりしてしまったのだ。
何のことはない、この教師こそ、「問題文の意味を理解せず」「意味のない式を書いてしまう」人物だったのだ。
その後、僕に注意されて間違いに気づき、正しい式を書きはじめた。ところが、最初に「3×」と書いた直後、手がぴたりと止まってしまった。次に「2」と書くべきか「3.14」と書くべきか分からなくなったのだ!
かけ算順序固定派のルールでは、最初に書く字は回答と同じ単位の数字と決まっている。この場合、求めるのは円の円周（cm）だから、当然、最初は3（cm）である。だが、2番目、3番目の数字についてのルールがない。これまでずっとマニュアル通りに問題を解いてきたの「で、マニュアルにない問題を突きつけられたとたん、混乱してしまったのだ。
その教師は悩んだ末、「3×2×3.14」という「正解」を書いた。しかし、数学の公式では円周の長さは2πrである。賢い子供なら、すでに公式を知っていて、それに従い「2×3.14×3」と書いてもおかしくない。しかし、そう書いたら、かけ算順序固定派の教師に×にされてしまうのだ!
事実関係において見過ごせないものがあります。「かけ算順序固定派のルールでは、最初に書く字は回答と同じ単位の数字と決まっている。」の文です。算数教科書や学習指導案より，反例を見ることができます。「段数×４＝周りの長さ」の件で，次期の算数解説に取り入られました*2。この事例のほか，長方形・正方形の面積の公式も考慮に入れると，被乗数と積とが異なる種類の量になり得ることは，4年で学習します。円周の長さや円周率よりも前です。「最初に書く字は回答と同じ単位の数字」，言い換えると「被乗数と積は同種の量」というのは，著者が忖度するものではなく，2年および3年の出題・学習をもとに経験的に得られるものです。
それはそれとして，上記に「円周」が4回，出現することを起点に，話を掘り下げてみることにします。というのも，そのうち3回は，「円の円周」となっています。最初の「半径3cmの円の円周の長さを求めなさい」は，「半径3cmの円」の「円周の長さ」と解釈すればいいのですが，あとの2つの「円の円周」は，単に「円周」でよいはずです。
「円」と「円周」，それから「円周率」をどのように書いているのか知るため，手元の2冊の紙媒体で，調べてみました。
まずは『算数教育指導用語辞典 第四版』*3です。出現ページとその記載を箇条書きにします。「//」は改段落を表します。
- p.95: 平面上で，ある定点から等距離にある点の集まりとみられる曲線，または，この曲線の内部を含めた全体の形を円という。この定点を円の中心といい，円をふちどっている曲線を円周という。
- p.100: 5年で，円周の長さと直径の長さの関係を調べ，円周の長さが直径の長さの何倍になっているかを調べさせている。その何倍かを表す数を円周率という。
- 同: [1] 関数の考えを育てる一場面 // いろいろな大きさの円，すなわち，直径（半径）の異なるいくつかの円を並列的に見て，何が変化しているか，逆に，何が変化していないのかに着目させ，直径の長さと円周の長さを変数として見られるようにしていく。
- 同: [2] 測定で円周率の意味を知らせる // 実際にいくつかの具体物で円の直径と円周を測定し，どんな大きさの円についても，円周の直径に対する割合が一定であることを見出すようにする。その体験的な気づきをもとに，指導していく。
- 同: 円周率 // the ratio of the circumference of a circle to its diameter, circle ratio（π） // 円周の長さが直径の長さの何倍かを表す数を円周率という。円周率（π）は，どんな大きさの円でも一定の値をとる。円周率は，詳しくは，3.1415926535897932384626…のようにどこまでも続く。その数の並び方は，循環小数のようなきまりは見られない超越数といわれるもので，わり算で求められる数でない。ふつう3.14が近似値として用いられる。
- p.279: 円の性質 // 円をふちどっている曲線を円周（用語は5年），中心と円周上の点を結ぶ線分を〔以下略〕
- p.309: 円について，円周の直径に対する割合（円周率）が一定であることを知り，円周・直径・円周率の関係を明らかにする。
2冊目の本は，『算数・数学用語辞典』*4です。
- p.22: 円 えん [circle] // コンパスで描いた曲線が囲む平面の一部を円といいます。また，この曲線を，この円の周といいます。円の周の一部を弧といいます。// コンパスを使わない一般的な定義は次のようになります。// 平面上の1点Oから等距離にある点は，1つの曲線を描きます。この曲線を囲む平面の1部を円といい，点Oを，この円の中心といいます。また，この曲線を円周といいます。〔以下略〕
- p.23: 円周 えんしゅう [circumference] // 円を囲んでいる曲線を，円周といいます。〔以下略〕
- p.23: 円周率 えんしゅうりつ [ratio of circumference of circle to its diameter] // 円周の長さと直径の長さとの比を円周率といいます。円周率は，回りを表すギリシャ語ペリフェレイア〔ギリシャ語のため省略〕の頭文字をとって，π（パイ）で表します。// π＝3.141592653589732384… // が知られています。計算機の進歩によって，現在，その値は2兆桁を超えて計算されています。
とりあえず，「円の円周」という表記については，どちらの本にも出現しませんでした。「円をふちどっている曲線を円周という」「この曲線を，この円の周といいます」のように，円周の概念の導入にあたっては，書き方に配慮のあとがあるのも，読み取れます。
Webで読むことのできる情報として，wikipedia:円周を見ておきましょう。簡潔な定義は「円周（えんしゅう、英: circumference）とは、円の周囲もしくは周長のこと。円周と直径の比率を円周率という。」となっています。図の直後には「円の周長cは」，また円周と面積の説明において「円周を円の半径rについて」といった表記も見られます。「円の」が「円周」に係るような使い方には，なっていません。
教師とのやりとりに戻る前に，円周率について検討しておきます。wikipedia:円周率では「円周率（えんしゅうりつ）は、円の周長の直径に対する比率として定義される数学定数である」と書かれています。『算数・数学用語辞典』では「円周の長さと直径の長さとの比を円周率といいます」ですし，「比」の文字を入れた円周率の定義は，コトバンク*5，goo国語辞書*6，weblio辞書*7でも見ることができます。
それに対し，『算数教育指導用語辞典 第四版』では，「円周の長さが直径の長さの何倍かを表す数を円周率という」や「円周の直径に対する割合*8」のように，「比」を使用していません。
もちろんこれは，「比」は6年で学習するので，5年で円周率を学ぶ段階において利用できないことが関係しています。かわりに，「何倍か」や「割合」を用いています。とくにp.309では，割合を学習する中での円周率の扱いが記されています。小数のかけ算・わり算とともに，割合の概念を学習しておけば，図形にも適用できるというわけです。
「割合＝くらべる量÷もとにする量」により，割合を求めたとき，「くらべる量＝もとにする量×割合」という式が使えます。円を対象とするなら，もとにする量は直径で，くらべる量は円周，そして割合は，円周率です*9。
教師とのやりとりで著者が与えた問題，「半径3cmの円の円周の長さを求めなさい」について，直径は3cmの2倍ですから3×2と表せます。そして割合の第2用法と，円周率を3.14とすることにより，（3×2）×3.14，または3×2×3.14という式になります。あとは計算なのですが，3.14×6を筆算することで，18.84が求められます。答えは「18.84 cm」です。
立式の根拠となる，公式（言葉の式）は，「円周＝直径×円周率」と「直径＝半径×2」です。
ところで，p.38における「数学の公式では円周の長さは2πrである。賢い子供なら、すでに公式を知っていて、それに従い「2×3.14×3」と書いてもおかしくない」は不可解です。小学校では2πrのような，乗算記号を省略した式は扱いません。中学の数学を先取りしている「賢い子供」なら，2πrと学んだ上で，小学校では「直径×円周率」の公式で式を立てることを，想定すべきでしょう。
（最終更新：2018-03-05 晩）
*1:メインブログではhttp://d.hatena.ne.jp/takehikom/20141004/1412352292で取り上げました。Kindle版はasin:B0739MD1JSです。
*2:http://takexikom.hatenadiary.jp/entry/2017/09/11/215947
*5:https://kotobank.jp/word/%E5%86%86%E5%91%A8%E7%8E%87-38162：「平面上の円の円周と直径との比の値」
*6:https://dictionary.goo.ne.jp/jn/26415/meaning/m0u/%E5%86%86%E5%91%A8%E7%8E%87/：「円周の、直径に対する比」
*7:https://www.weblio.jp/content/%E5%86%86%E5%91%A8%E7%8E%87：「円周の直径に対する比の値」
*8:現行および次期の『小学校学習指導要領解説算数編』にも，出現します。
*9:言葉の式で表すと，「円周率＝円周÷直径」となります。https://style.nikkei.com/article/DGXMZO80396050S4A201C1000000にも「円周÷直径」が出現します。
単位なしの立式はミスのもと?
- https://twitter.com/yamasati39/status/968061933495640064*1
「単位なしの立式はミスのもと」には賛同できません。次元解析や組立単位を，小学校の算数に適用することは，個人的にふさわしくないと考えているからです。
式に単位を入れることについては，メインブログで以前にまとめていたので，取り出しておきます*2。「45人で，講堂にイスを運んでいます。1人が1個ずつ4回運ぶと，みんなでイスは，何個運ぶことになるりますか」という文章題に対し，現在，小学3年生に出題するなら，期待される式は，「4×45＝180」です。
単位を入れた立式となると，「4個/人×45人＝180個」が考えられます。この式では「個/人」も，一つの単位となります。他の可能性として，「4個×45人＝180個」も，分からないではありませんが算数・数学的に好まれません。かつては「4個×45＝180個」のように，かけられる数と積に単位を明記し，かける数は（問題文では「45人」とあっても）「45」と無名数にする，というスタイルもありました。
「単位ありの式」は，加減乗除で利用できます。たし算やひき算の式では，どの項も，また計算結果も，同種の量とし，同じ単位をつけます。お花の数なら「2ほん＋3ほん＝5ほん」，人数の増減なら「13にん－8にん＋5にん＝10にん」などです。
導入時（2年）で学習するかけ算では，「3こ/さら×5さら＝15こ」といった表記になります。かけられる数の単位は「a/b」と書かれ，「3こ/さら」は，1皿にリンゴが3個ずつ乗っている状況などを表します。かける数の単位は「b」で，かけ算により，単位が「a」の量が得られます。これは日本独自というわけではなく，Schwarz*3やKaput*4も，理論化ならびに実際の教育への適用を試みています。それらの文献で，「こ/さら」「さら」「こ」に対応する概念は，dimensionでもunitでもなく，referentと呼ばれます。次元解析*5では通常，対象とする量は連続量ですが，referentにおいては分離量も許されます。
「3こ/さら×5さら＝15こ」の式をもとにすると，わり算には2種類の式のパターンが考えられます。一つは，「15こ÷5さら＝3こ/さら」のように，1あたり量を求めるわり算です。もう一つは，「15こ÷3こ/さら＝5さら」のように，1あたり量がわる数になる場合です。前者は等分除，後者は包含除に対応します。なお，面積計算や直積の計数では，ここまで書いてきたのと異なるタイプのかけ算となりまして，式に，「/」を含む単位が出現しません。
「単位なしの立式はミスのもと」については，「立式するときは必ず単位をつけましょう」ではなく，「立式するときに単位をつけて書くと便利ですよ（ミスが減りますよ）」という意味だと考えられます。しかし，そのように解釈するとしても，算数の具体的な問題における適用に関して，十分に考慮されてきたとは思えません。
例えば，面積や直積などでない，言い換えると被乗数と乗数の違い（非対称性）があるかけ算でも，単位を書くと手間が増え，その一方で式の正しさや計算の用意さを支援しないような場面が考えられます。2年で学習する倍概念がその最初で，例えば，「6cmの2ばい」をかけ算の式で表す場合，「6cm×2ばい」では積の量が不明瞭（「cmばい」は明らかにおかしい）であり，かといって「6cm/ばい×2ばい」と書くわけにいきません。数学教育協議会の方々の著書を読んできた限り，この倍概念については，「6cm×2」と表しており，「3こ/さら×5さら＝15こ」のタイプのかけ算より，学習における優先度が下げられています。
面積計算においても，4年で学習する正方形や長方形の面積，またそれらの複合図形くらいであれば，「○cm×△cm＝○×△㎠」は有用かもしれませんが，5年の台形で「（2cm＋3cm）×6cm÷2」，6年の円で「3cm×3cm×3.14」と書いてみると，どうでしょうか。そして，これらにおいても組み合わせたり一部をカットしたりした図形の問題まで考慮すると，立式（答案に書くかどうかはさておき）における単位の有用性を主張するにも，限界があるように思います。
そして，昨年公開された『小学校学習指導要領解説算数編』*6が，「単位ありの立式」の不都合さに拍車をかけます。具体的には，第1学年の「異種のものの数量を含む加法・減法」と，第4学年の「伴って変わる二つの関係」が該当します。
「異種のもの」は，例えば，「お皿に1個ずつ，コップを乗せていきます。お皿は5枚，コップは7個あります。どちらがいくつ多いですか?」という文章題で，「7個－5枚」と書いてよいのか，よいとしたとき，差となる量をどう書けばいいのか，ということです。
「伴って変わる二つの関係」について，解説からは「（三角形の数）＋2＝（周りの長さ）」や「段数×4＝周りの長さ」を見つけることができます。前者の式の被加数と和は異なる量ですし，後者の式の被乗数と積も同様です。
後者はもう少し検討します。「段数を増やしていくと周りの長さがどのように変わるか」の件では，リフレッシュ研修８（変わり方） | 授業がんばりMATHの最も下の図形のように，変形することで，一つの正方形の長さは4cm，それがだんの数だけあるから，「4×段数＝周りの長さ」と表すこともできます。ここで「4」につけるべき単位は，段数の単位と長さの単位をもとに，「だん/cm」と表せます。10段のときの周りの長さは，図や表を用いることなく，「4だん/cm×10だん＝40cm」とできます。
ただし，『小学校学習指導要領解説算数編』の記載を読む限り，そのように表すことは，望まれていません。「だん/cm」という単位を認めない，というわけではありません。むしろ，小さな段数について，図を描いたり，2行の表にしたりすることで，帰納的に，「段数×4＝周りの長さ」を得ること，そしてこの式を得たら，10段でも100段でも，当てはめて計算すれば求められることが，ここでの学習の意義となっています。
*1:「ツイートは非公開です...承認された場合のみツイートを表示できます」と表示されます。
*2:http://d.hatena.ne.jp/takehikom/20130428/1367096291
*3:http://d.hatena.ne.jp/takehikom/20130312/1363031965
*4:http://d.hatena.ne.jp/takehikom/20111029/1319835106
*5:算数教育における文章題について書かれた中に，"Dimensional Analysis"の語が出現するものもあります。例えばhttp://books.google.co.jp/books?id=Vyl42R9JV1oC&pg=PA197より読めます。
*6:http://www.mext.go.jp/a_menu/shotou/new-cs/1387014.htmより，PDFがダウンロードできます。本記事ではhttp://www.mext.go.jp/component/a_menu/education/micro_detail/__icsFiles/afieldfile/2017/07/25/1387017_4_2.pdfの内容をもとにしています。
8×3を，表から見つける
- 山田剛史: 日常の問題に役立てたかけ算を数学内の問題に役立てる授業, 数学教育学の礎と創造―藤井斉亮先生ご退職記念論文集―, 東洋館出版社, pp.102-112 (2017). isbn:9784491034447
- 作者: 藤井斉亮先生ご退職記念論文集編集委員会
- 出版社/メーカー: 東洋館出版社
- 発売日: 2017/12/18
- メディア: 単行本
- この商品を含むブログを見る
数学内の問題に関して，「ねらい」(p.105)には，「23×3」や「23×5」といったかけ算の式が書かれています。いずれも，標準的には3年での学習です。例えば23×3なら，20×3と3×3に分けて計算をしてから加え，69を得ます。「一の位と十の位に分け」ることも，ねらいに含まれており，先取りの感もあります。
しかし本文を読む限り，20×3あるいは2×3や，3×3の答えを得るのには，九九を使用していません。代わりに活用されているのは，「かけ算の表」です。この授業より前につくられた，かけ算の表の写真が，p.104で以下のとおり，図となっています。
いずれも，2行・任意列の表です。どの表も，左端の上下には，異なる種類の量の名称が書かれています（「何枚」の「枚」のように，2年では学習しない漢字も，使用されています）。数の並びについて，上段は「1」「2」「3」…となっています。下段は，それぞれに対応する値ですが，マスの数に対する長さ(mm)のように，九九の範囲を超えている数もあります。累加により，右に伸ばしながら数値を入れていったものと推測でき，p.105には「本授業では「同数ふえセット表」と呼ばれている」が，カッコ書きにされていました。
ページを進めると，「かけ算の順序」の議論がありました(p.107)。
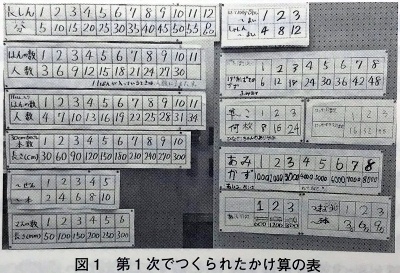
②8×3の答えを求める場面
教師が8×3の式を示し，学習者たちは答えを求めた。このとき，1人の学習者は積を24と求めるときに図2の丸で囲った箇所を使ったと発言し，もうひとりの学習者は図3の丸で囲った箇所を使ったと発言した。このことから「あの，何枚だと，～ちゃんの折り紙の答え方（図2の答え方）だと，3個目で24って出てるけど」「そっち（図2の答え方）だと，たぶん，みんな言っているのは，3×8しているのかな，と思ってる」と8×3は図3に示されているというかけ算の表現を誤って捉えている意見が出された。そこで教師から8×3は8＋8＋8，8が3こ，であることを伝え，8×3は図2の丸で囲った箇所であることが確認された。
引用した文のうち，「そっちだと，たぶん，みんな言っているのは，3×8しているのかな，と思ってる」は，ビデオ記録からの文字起こしで，カギカッコのない「8×3は図3に示されているというかけ算の表現を誤って捉えている意見が出された」は，著者による分析と考えられます。「そっちだと…」を言った子は，図3の丸で囲った箇所が8×3だと考えたが，その後の教師の発言により（いきなり否定はしなかったでしょうが）それは誤りと，読むことができます。
図1，図2，図3のいずれの表にも，共通点があります。「かける数」と「積」との対応表になっているのです*1。「かけられる数」は，明示されていないと言うこともできますし，上の行が1のときの，下の行の値が，実際には「かけられる数」になっています。これらに気づくと，図2の丸囲みは8×3＝24なのに対し，図3の丸囲みからは3×8＝24を，効率よく読み取ることができます。
ところで図2の上段左に何が書かれているのか，理解するのに苦労しました。どうやら「何こ」です。「何」の下に「～」と縦線があり，「1」と書いてしまったのを，波線で訂正したものと思われます。子どもが書いたのだと解釈すれば，「枚」を用いたことも，納得が行きます。
*1:「上の段×定数＝下の段」という捉え方は，この授業では期待されていません。学習するとすれば4年です：http://takexikom.hatenadiary.jp/entry/2017/09/11/215947。
a×b×cでもa×c×bでもよい
ある種の「かける順序を問わない場面」について整理します。小学校の算数で出題したとき，式は，a×b×cでもa×c×bでもかまいませんが，aが乗算記号の右に来ることは，期待されていません。
はじめに考える文章題は，以下のものです。「相似な図形の長さ」の応用題です。
82.8cmの直径の円があります。その3.23倍の直径の円の円周は何cmでしょうか。
円周率は3.14とします。答えとなる長さだけでなく，式も書くこととします。
素朴な求め方は，こうです。円周を求めたい円の直径は，82.8cmの3.23倍ですから，82.8×3.23で求められます。そして円周＝直径×円周率を使えば，円周は82.8×3.23×3.14と表せます。
電卓で計算してみますと，839.77416となりました。答えは839.77416cmです。小数点以下が細かすぎるようにも見えますが，1桁たりともおろそかにしないという方針のもと，計算させるのは差し支えないでしょう。
別の考え方もできます。82.8cmの直径の円について，先に，円周の長さを式にします。8.28×3.14です。そして，直径が2倍，3倍，…になると円周の長さも2倍，3倍，…になりますので，求めたい長さは82.8×3.14×3.23となります。計算結果（839.77416）は変わりません。
この文章題は，以下の文献で取り上げられています。「教授学の探究」は大学の紀要と思われますが，著者は小学校教師です。
- 佐藤敬行, 問題づくりを通して乗除演算の意味を考える―「いろいろな文章問題」（小学校5年）の実践から, 教授学の探究, 北海道大学大学院教育学研究科教育方法学研究室, Vol.23, pp.27-54 (2006). http://ci.nii.ac.jp/naid/120000964041 http://hdl.handle.net/2115/13659
本文に，授業中のやりとりも載っています(pp.31-32)。「 」が先生，『 』が子どもの発言として読めば，話が合います。
「（2）の式は?」『82.8×3.14×3.23』「え，ちがうよ，（82.8×3.23）×3.14だよ。かける順番を逆にしても結果は同じだけど，式としては間違いだよ。まぎらわしいんだよな，数値が。でも考え方は（82.8×3.23）×3.14だからね」
高学年の小数の計算でも，かけ算の順序に注意して指導しているのかと思いながら，読み進めると，その直後に，後日談がカッコ書きとなっていました。
（後に気がついたことだが，直径が3倍になれば円周も3倍になると考えると両方とも同等に正しい。）
冒頭の文章題に対して，82.8×3.14×3.23あるいは（82.8×3.14）×3.23の式もまた，正解になる，というわけです。
ただし，「両方とも同等に正しい」であり，「どんな順番でもよい」と言っているわけではない点にも注意が必要です。3つの数の積で，どんな順番でもよいような事例として，直方体の体積（縦・横・高さ）が考えられますが，それとは状況が異なります。
なぜ「どんな順番でもよい」ではないのかを考えるにあたり，正解となる（カッコを使用しない）2つの式は，ともに「82.8×」から始まっている点に注目したいところです．これは最終的に求めたい（円周の）円とは別の，円の直径です。かけ算の式を立てる際の，出発点となるのが，「82.8」だというわけです。
次の文章題も，ここまで書いた性質を持っています。
5人家族があります。それぞれ，1日に3個ずつ，ミニトマトを食べます。7日間で，この家族は全部で何個のミニトマトを食べるでしょうか?
解答は難しくありません。5人家族で1日に3個ずつ，ミニトマトを食べるというので，この家族が1日に食べるミニトマトは3×5＝15で15個です。7日間ですから，15×7＝105 答え105個となります。一つの式で表すと，3×5×7＝105です。
別の考え方もできます。1日に3個ずつ，7日間ですから，1人が食べるミニトマトは3×7＝21で21個です。5人いますので，21×5＝35 答え105個となります。一つの式だと，3×7×5＝105です。
この場合にも，式の最初の3であり，5や7にはなりません。この3は，「1人が1日に3個」，ミニトマトを食べるということと対応します。パー書きで表すと，「3個／人・日」です。https://www.nmij.jp/public/report/translation/IUPAC/より読むことのできる『物理化学で用いられる量・単位・記号 第3版』の表記を，個や人や日といった分離量の単位にも適用するなら，「」と表せます。ともあれ以下では「3個／人・日」をはじめ，パー書きを用います。
3×5×7＝105という式に出現する，それぞれの数に，単位を付けると，「3個／人・日×5人×7日＝105個」となります。3×5＝15については，「3個／人・日×5人＝15個／日」で，5人家族で1日あたり15個食べる，と解釈できます。
3×7×5＝105の式に対しては，「3個／人・日×7日×5人＝105個」であり，3×7＝21は「3個／人・日×7日＝21個／人」（7日間で1人あたり21個食べる）です。
3×5×7のうちの5×7を，そして3×7×5のうちの7×5を，先に計算することも可能です。その積は，「35人・日」ですが，「35食」と読み替えることにします。1食で3個ずつ，ミニトマトを食べるとすると，35食分に必要なミニトマトの数は，「3個／食×35食＝105個」と表せます。
ミニトマトの数については，1人が1日に食べる数を固定としたとき，人数と日数の両方に比例します。複比例です。その定数（複比例定数）は，1人が1日に食べる数であり，ここでは「3個／人・日」となるのでした。「人・日」を「食」に置き換えることで，「1あたり×いくつ分」が適用可能になった，というわけです。
それでは，はじめに書いた，2つの円の問題では，求めるべき円周の長さは，もとの円の割合と，円周率の2つに比例すると言って，よいのでしょうか?
2つ，難点があります。一つは「円周率に比例する」と言うと，まるで円周率が変量（説明変数）であるかのようですが，その解釈は自然でない*1こと，もう一つは，82.8×3.23×3.14における3.23×3.14や，82.8×3.14×3.23における3.14×3.23について，その積（形式的には10.1422で，無次元量です）に，「35人・日」または「35食」と同様の，量的な意味を与えるのが困難であることです．
2つの文章題から考えることのできるかけ算の関係を，乗法的オペレータ*2に基づき，図にしてみます。ミニトマトの件は，以下のようになります。
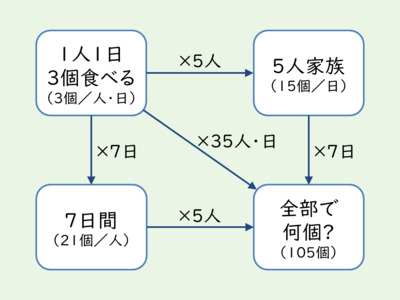
2つの円については，以下のとおりです。右上・左下・右下の計算結果（それぞれの長さ）は省略しています。もとの円の直径から，求めたい円周への矢印がないのは，先ほど書いた難点の2番目が理由となります。
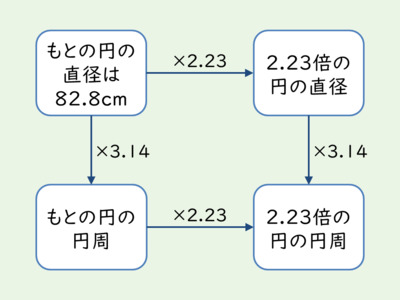
啓林館の算数6年の教科書にも，類題があり，さまざまな立式を含む授業例が報告されています。
画像より読むことのできる文章題は「たけしさんは7人家族です。災害に備えて，全員の3日分の水をそろえようと思います。1.5L入りのペットボトルを何本買うとよいでしょう。」です。そこに「1人1日に必要な水の量は3Lとします。」を付け加えれば，式を立てて計算し，「42本」という答えを得ることができます。
2行3列で6個の式が，1つの画像になっています。総合式*3だと「3×7×3÷1.5」「3×3×7÷1.5」「3÷1.5×3×7」，分解式だと「3×7＝21 21×3＝63 63÷1.5＝42」「3×7÷1.5＝14 14×3＝42」「3×3÷1.5＝6 6×7＝42」です。いずれにおいても，最初の数は3で，「1人1日に必要な水の量は3L」に対応します。
本文では「最初に7×3をして，「のべ21人分必要」ということから処理することもできるが子どもはしないでしょう。」がカッコ書きされています。「のべ」が時代を感じさせます。
「ミニトマト」および「相似な図形の長さ」については，メインブログの記事もご覧ください。
*1:「直径に円周率をかけると円周になる」と言うのは，差し支えありません。このことは「比例」と「かけ算」との違いとして，別の機会に再検討したいものです。
*2:http://www.shinko-keirin.co.jp/keirinkan/sansu/WebHelp/03/page3_12.html
*3:総合式と分解式の違いについては，例えばhttps://www.shinko-keirin.co.jp/keirinkan/sansu/WebHelp/03/page3_05.htmlで書かれています。『小学校学習指導要領解説算数編』には，「総合式」「分解式」のいずれの用語もない代わりに，第4学年で「四則を混合させたり（ ）を用いたりして一つの式に表すことには，数量の関係を簡潔に表すことができるなどのよさがあることが分かるようにし，四則を混合させたり（ ）を用いたりして一つの式に表すことができるようにすることが大切である。」と書かれており，総合式の意義は，その学年で学ぶべきとされています。
わり算の順序
6÷3＝2ですが，3÷6を計算せよとなると，まず思い浮かぶのは0.5です。分数で答えるなら，約分してが考えられます。
a÷bとb÷aとで，答えが違ってきます（a＝bのときを除いて）。文章題で，一方の式が正解，他方が間違いというのが，小学校5年を対象とした調査で使用されています。答えは違うものの，そこから得られるものは同じだという事例もあります。
1. 8÷4ではなく4÷8
調査問題として，まず紹介したいのは，「8mの重さが4kgの棒があります。この棒の1mの重さは何kgですか。求める式と答えを書きましょう。」です。2010年（平成22年度）実施の全国学力・学習状況調査，算数A大問2の(1)です。
わり算で求めるのですが，8÷4＝2としたら，1kgの重さが2mとなってしまいます。正解となる式は，4÷8です。答えは0.5(kg)ですが，8分の4のように，約分していない分数も，正解扱いとされています。
正答・誤答の状況は，国立教育政策研究所のサイトで公開されており，以下より知ることができます。
- 全国学力・学習状況調査の「報告書・集計結果資料（2010年7月30日）」
- 「平成２２年度 全国学力・学習状況調査 報告書・集計結果」についての「２ 平成２２年度 全国学力・学習状況調査【小学校】報告書」
- 平成２２年度 全国学力・学習状況調査【小学校】報告書の「(2)算数（PDF：7.3MB）」
- https://www.nier.go.jp/10chousakekkahoukoku/02shou/shou_4s.pdfで，p.148に問題文と正答率，次のページに解答類型と反応率の表
- 平成２２年度 全国学力・学習状況調査【小学校】報告書の「(2)算数（PDF：7.3MB）」
- 「平成２２年度 全国学力・学習状況調査 報告書・集計結果」についての「２ 平成２２年度 全国学力・学習状況調査【小学校】報告書」
解答類型と反応率の表によると，式が「4÷8」，答えは「0.5と解答しているもの」が54.1%，そして同じ式で答えは「と解答しているもの（大きさの等しい分数を含む）」が0.0%となっています。誤答については，式が「8×4」を，答えは何であってもひとまとめとし，反応率は31.1%です。
この3年後に実施の中学Aに「aメートルの重さがbグラムの針金があります。この針金1メートルの重さは何グラムですか。a，bを用いた式で表しなさい」という問題があり（この正答率は33.7%），その解説の中にも，小学校の棒の重さの問題は正答率54.1%と書かれていました。
2010年調査の算数の解説には，「商が1より小さくなる等分除（整数）÷（整数）の場面では，何が被除数で何が除数かをとらえることが困難な場合がある。そのような場面からも，数量の関係をとらえ，除法を用いることを判断できるようにすることが大切である」とあり，2013年調査の数学の解説には，「問題文に登場する数量の順に，aメートルをbグラムでわればよいと捉えた生徒がいると考えられる」と分析されています。
これらの，いわば「わり算の順序」を問う問題では，4÷8か8÷4か，（a分のb）か
（b分のa）かに，焦点を当てることができます。個人的には，これらが正解できるようになるために，「かけ算の順序」も必要だと主張するよりは，非可換である減法・除法のみならず，（増加の意味の）加法や，（累加や割合に基づく）乗法では，演算対象となる2つの数量には違いがあるわけで，それを踏まえて，子どもたちが場面を把握できるようさまざまな出題が作られており，授業やテストで問われてきた，と認識しています。
海外にも，同様の出題が見られます。文献は以下のとおりです。
- Fischbein, E., Deri, M., Nello, M. S. and Marino, M. S. (1985). The Role of Implicit Models in Solving Verbal Problems in Multiplication and Division. Journal for Research in Mathematics Education, Vol.16, No.1, pp.3-17. http://www.jstor.org/stable/748969
この文献のTable 1では，12個のかけ算と14個のわり算の文章題が，表になっています。このうち16番目は，"15 friends together brought 5 kg of cookies. How mush did each one get?"という文章題です。
Table 3を見ると，「5÷15」の正答率が第5学年で20%です。誤答のうち「15÷5」が68%を占めます。第7学年・第9学年の生徒にも解いてもらっており，学年にともない正解率は上がりますが，第9学年でも半数以上が15÷5を解答しています。
大きい数÷小さい数，ではなく，わって得られる値が何を意味するのか，文章題で問われていることと合致するかが，国内外で検証されてきたと言えます。そして，昭和26年の小学校学習指導要領算数科編（https://erid.nier.go.jp/files/COFS/s26em/chap5.htm）で指摘された，「こどもは問題に出てくる数を，その数の意味を深く考えもしないで，出てくる順に書き並べ，その間に，かけ算記号を書き入れることがわかった」が，わり算でも通用することを示唆します。
かけ算の順序が問われるのは，主に2～3年です。わり算は，3年で学習しますが，そこでは4÷8や5÷15といった式を立てる機会はありません。わり算の順序は，割合や小数の乗除を学習する5年の段階で出題されてきたわけです。「かけ算の順序」と「わり算の順序」とを同列に扱えない，と言うこともできます。
2. 6÷20と20÷6，答えは違うけど，どちらで計算しても結論は同じ
「a÷bとb÷a，答えは違うけど，それぞれに意味がある」，そして「どちらのわり算でも，同じ結論になる」という事例を紹介します。
- サルカール アラニ・モハメッド レザ: 算数・数学教育における子どもの概念形成と思考方略―イラン、アメリカ、日本の比較授業分析―, 中等教育研究部紀要, 名古屋石田学園, Vol.2, pp.3-30 (2010). https://cir.nii.ac.jp/crid/1571417127872017792 http://www.n-ishida.ac.jp/main-office/tyuto/kenkyukiyou/09/P3.pdf
イランとアメリカは「かけ算の順序」，日本は「わり算の順序」に関する授業です（かけ算の順序を授業にすると～イランとアメリカ - わさっき）。日本の授業は，5年の算数です。「Aは6平方mで20人います。Bは4平方mで15人います。どちらが混んでいるでしょうか。」という出題が，中心になっています。
「どちらが混んでいるでしょうか」というのは，混み具合です。1平方mあたりの人数に直すと，Aは20÷6＝3.33...，Bは15÷4＝3.75で，1平方mあたりの人数はBのほうが多く，したがって，混んでいるのはBだ，というのが想定される答えの一つです。
わり算を逆にすると，計算結果が違ってきます。Aは6÷20＝0.3，Bは4÷15＝2.66...です。そしてこれは，1人あたりの面積です。1人あたりの面積はBのほうが小さく，ここからも，混んでいるのはBだと言えます。
わる順序を逆にすると，得られる商の意味は変わり，大小関係も反対になります。1平方mあたりだと，3.33...＜3.75で，1人あたりだと，0.3＞2.66...です。そして，混み具合としては，1平方mあたりの人数が多いほう，1人あたりの面積が小さいほうが，「混んでいる」というわけです。
ここまで割り切れないときには「...」を書いてきました。1平方mあたりの人数を求めるのだと，Aでは割り切れず，1人あたりの面積を求めるのであれば，Bでは割り切れません。これは，割り切れるほうでわり算（わる数）を揃えさせない意図的なものだろうと思いながら，『小学校学習指導要領解説算数編』を見ると，現行および次期のPDFには「10平方mの部屋に7人いる場合と15平方mの部屋に10人いる場合について混み具合を比べる」が書かれていました。5年です*1。この例でも，1平方mあたりで比べるのであれば，「15平方mの部屋に10人」のほうの10÷15が割り切れず，1人あたりで比べるのであれば，「10平方mの部屋に7人」について10÷7が割り切れません。
一つ前の解説（1999年）については，書籍[isbn:9784491015507]を見ました。単位量当たりの大きさは6年でしたが，具体的な数を用いた場面の提示はありませんでした。
AとBの混み具合の授業について，サルカール アラニによる紀要の脚注34に，出典が書かれており，少し調べると，以下の本にたどり着きました。Amazonで購入可能となっていますが高額です。
- 帝塚山学園授業研究所: 小学5年・よい授業の条件―みどころと改善点, 明治図書出版 (1988). [isbn:4182345002]
「a÷bとb÷a，答えは違うけど，それぞれに意味がある」とはいっても，「8mの重さが4kgの棒があります。この棒の1mの重さは何kgですか」の問いに対して8÷4＝2と計算し，答えとして「2kg」「2m」「2m/kg」のどれを書いても正解とならないのにも，注意したいところです。
3. 速さ＝道のり÷時間でなければならないのか?
「はじき」または「みはじ」と呼ばれる公式があります。メインブログでみはじ・くもわ (2015.08) - わさっきというまとめを作成しています。当ブログでは今年，アンチはじきという記事を書いてきました。
次期の『小学校学習指導要領解説算数編』では，（速さ）＝（長さ）÷（時間）という式が例示されています。ただし，長さを求める式や，時間を求める式の記載はありません。
「時間÷長さ」を速さとすることも，可能ではあります。解説では，「一方で日常生活などでは，速さを，一定の長さを移動するのにかかる時間として捉えることがある。例えば100m走などの競技では，100mを走るのにかかる時間によって速さを表している。時間が短いほど，速さが速いということになる。（略）速さを，一定の長さを移動するのにかかる時間として捉えると，速いほど小さな数値が対応することになる。」と記しています。ただしこの続きは，「一般に速さについては速いほど大きな数値を対応させた方が都合がよいため，時間を単位量として，単位時間当たりの長さで比べることが多い。」でして，やはり速さの公式は「速さ＝長さ÷時間」となります。
「速さ＝長さ÷時間」が一般的だけれど，わり算の順序を反対にして「時間÷長さ」も，速さに関する量となるのだ，とみると，混み具合も同様です．人口密度と言えば，1平方kmあたりの人数ですが，面積を人数でわることでも，混み具合を算出し，比較に使えるのです。
また別の，異種の二つの量の割合として，単価があります。aメートルでb円の布の単価はと問われると，1メートルあたり何円かと考えるのが自然であり，式は，b÷aです。
ですが，1円で何m買えるのかを，単価とするのなら，a÷bという式になります。
駐車料金を対象として，以下の記事で，検討を試みました。
その検討から，いくつか言葉の式を，得ることができます。まず，「単価［円/分］＝料金［円］÷駐車時間［分］」により，単価を定義するのなら，そこから「料金［円］＝単価［円/分］×駐車時間［分］」および「駐車時間［分］＝料金［円］÷単価［円/分］」という式も導けます。
次に，わり算の順序を逆にします。「単価'［分/円］＝駐車時間［分］÷料金［円］」と定義します（「単価［円/分］×単価'［分/円］＝1」「単価［円/分］＝1÷単価'［分/円］」でもあります）。すると，「駐車時間［分］＝単価'［分/円］×料金［円］」および「料金［円］＝駐車時間［分］÷単価'［分/円］」が導けます。
単価［円/分］を用いた3用法では，料金［円］はかけ算で，駐車時間［分］はわり算で求めます。それに対し，単価'［分/円］に基づく3用法では，駐車時間［分］はかけ算で，料金［円］はわり算で求めます。かけ算とわり算が，反対になっていますが，ともあれ具体的な数を与えられれば，計算はできますし，それぞれの3用法が，かけ算が1つでわり算が2つで構成されているのも，共通しています。
わり算の順序を反対にしても，問題なく計算できます。しかしながら2種類の3用法にまとめ上げることは，小学校の算数の範囲外と言わざるを得ません。
ここでの検討を，小学校の算数に反映させるなら，わり算を逆にして得られる，2つの単位量あたりの大きさが，逆数となる点でしょうか。「8mの重さが4kgの棒があります」を前提として，この棒の1mの重さは，0.5kgですが，1kgの長さは，2mであり，パー書きの量を用いて0.5［kg/m］×2［m/kg］は1（無次元量）となります。Fischbeinらの"15 friends together brought 5 kg of cookies."についても，［kg / person］×
［person / kg］＝1です。
2022年6月追記
「わり算の順序」「全国学力テスト」について，2018年以降に作成したうち本記事に関係しそうなものを挙げておきます。
*1:ただし，その後を読むと，公倍数の使用が推奨される展開となっています。サルカール アラニ(2010)に書かれた，AとBの混み具合の件だと，6と4の最小公倍数をもとに，12平方mの人数で比べることになります。Aは，6平方mを12平方mにするので，人数も2倍して20×2＝40です。Bは，4平方mを12平方mにするので，人数は3倍で15×3＝45と求められます。12平方mあたりにすると，Aは40人，Bは45人だから，Bのほうが混んでいます。この計算では，小数の乗除は使わないものの，倍数・最小公倍数のほか，比例関係（面積をp倍して，同じ混み具合にするには人数もp倍する）も必要とします。やはり，5年の学習事項です。
積の非可換性について
行列と，みかんの数などを求めるためのかけ算（の順序）とを対比するのではなく，算数・数学教育に関心を持ち，これまでの成果を踏まえて建設的な議論をするには，「拡張」について，認識しておきたいところです。
このツイートを目にして，思い浮かんだのは「四元数」です。以下の本は，算数を専門とする小学校の先生なら，おそらく持っているでしょう。
- 作者:日本数学教育学会出版部
- 出版社/メーカー: 教育出版
- 発売日: 2009/02/01
- メディア: 単行本
ここのpp.18-19に「形式不易の原理」が書かれています。「1 数の拡張の考え」「2 形式不易の原理」「3 形式不易の原理の素地」で構成されます。非可換（交換の法則は成り立たない）が明記されている，p.19の段落を書き出します。
H.ハンケル（1839～1873）は，ピーコックの不完全さを見直したうえで，さらにこの原理が拡張された実数系や複素数系にまで及んで成立することを示した。さらに，原理に示された三つの計算法則は，高々複素数の範囲までに止まることを示し，さらにその拡張が多元数に及ぶときは，これらの三つの法則どれかが不成立になることを示唆している。例えば，多元数のなかでW.ハミルトンの四元数については交換の法則は成り立たない。また，A.ケーリーが示した八元数の場合では，交換法則のほかに結合法則も不成立となるのである。
「三つの法則」とは，交換法則・結合法則・分配法則のことです。
いったんこの本より外に，情報源を求めますと，wikipedia:四元数では定義や性質，また歴史的なことも記載されていますし，四元数は，2×2の複素行列，または4×4の実行列で表すことも書かれています。単射環準同型であることと，（そこで表現されている）複素行列・実行列の積が一般に非可換であることからも，四元数の積は一般に非可換であるのが分かります。
交換法則（可換性）と別で，拡張によって，それまでの性質が満たさなくなるものも，いろいろ考えられます。小学校の範囲であれば，わり算は，その導入において「商はわられる数よりも小さい」*1ことを知ることもできますが，5年で，1より小さい数でわる場面を通じて，成立しないことを学びます。
なお，有理数の範囲で成立しないとしても，わられる数は0より大きく，わる数が1より大きいという有理数においては，「商はわられる数よりも小さい」は成立します。同じように，行列でも四元数でもかまいませんが，一般に積は非可換だけれど，複素数と同型の集合に限れば，可換になり得る*2，ということもできます。
ひき算の結果はひかれる数よりも小さいことの反例は，中学の負の数を学ぶ段階となります。中学までと高校との違いといえば，実数までは通常の大小関係によって全順序集合となるけれども，複素数では同様の全順序集合にならない*3，簡単にいうと虚数単位iについてi＞0とi＜0のどちらを採用しても都合が悪いことが，思い浮かびます。
『算数教育指導用語辞典』のpp.18-19の脚注に「計算法則に関する注意事項」が記されています。「三つの（計算）法則」また「かけ算の順序」への言及がなされているとともに，国内外の算数教育の知見であると考えられます。かけ算・資料集1（2010年までの書籍） - わさっきより，転載します。ミカンとみかんの混在は，原文ママです。
計算法則に関する注意事項
数の拡張では，三つの計算法則の確かめが必要であったが，これはあくまでも形式であって，これと離れた具体的な場面では注意すべきことがある。
例えば，交換法則に関しては，同じ加法でも合併なら交換が可能であるが，追加（増加）の場合では交換は不可能である。例えば，ミカンが5個あっても3個もらうと8個になるということから，3個もらって5個あってというのは意味が曖昧になってしまう。不用意に交換すると時間差を無視したりすることになる。
また，乗法で，被乗数と乗数を交換しているのは，2次元的な面積の場合が，縦横同じ種類のものが並んでいる人間とかおはじきなどの数を求める場合はわかりよい。
ただし，この場合でも，被乗数と乗数を交換したとき，その基準量をどうとらえたか，操作の観点をどこに置いたかをよく考え，その違いをはっきりとつかんでおかねばならない。同数累加や倍概念で操作する1次元的な乗法では，安易な交換は許されない。
例えば，三つの皿にみかんが2個ずつあるとき，みかん全部の個数は2×3で求められる。しかし，皿の数三つにみかんの数2個をかけて3×2というのは意味がなく，このような具体的な場面で2×3が3×2に等しくなることを理解させるのは，かなり無理があると考えられる。
積を求める際に2つの“因数”が異なる場面として，算数では3年で学習する「乗数又は被乗数が0の場合の計算」が知られています。的当てゲームで，0点のところに3回当たったときの式を「0×3」，3点のところに1回も当たらなかったときの式を「3×0」と表すことができます。2つの因数の位置が変わっただけのようにも見えますが，前者については0×3＝0＋0＋0＝0と累加で求めたり，「0＋0＋0」の具体的な場面を考えたりできるのに対して，後者を累加で意味付けるのは困難です。「0」を数学の文脈でいうと，零元です。ベクトルでも行列でも四元数でも，零元の任意倍と，任意の元の0倍について，結果はどちらも零元になりますが，表記上も意味上も，別物として扱われます。
どこで交換法則が利用可能でありどこには使われない（小学校算数での適用が期待されない）かについては，今年，図示を試みました。
拡張に関しては，東京新聞「掛け算の順序論争再燃」を読んで思ったことで少し言及しました。冒頭の方の別のツイートは，「20分／500円」から，駐車料金と最大駐車時間を計算してみるでも使わせていただいております。
*1:わる数が，乗法の単位元1のときには，わられる数と商が等しくなるので，きちんと言うなら「商はわられる数よりも大きくない」となります。http://doi.org/10.24727/00027661よりダウンロードできる論文の結論に書かれた「×0，×1の学習指導は，「かけると常に大きくなる」いう思い込みを防ぐ役割を必ずしも担っていない」も興味深いところです。
*2:n次正方行列のうち「1行1列の成分は任意の複素数，それ以外の成分は0」「特定のi（1≦i≦n）に対してi行i列の成分は任意の複素数，それ以外の対角成分は1，残りは0」「単位行列の複素数（スカラー）倍」が該当します。
*3:wikipedia:順序集合には「複素数全体の集合Cには複素数の乗法と"両立"するような全順序は存在しない」とある点にも注意。
