「論究ⅩⅩ」(ローマ数字のⅩが2つで20),テーマは「「計算指導」に強くなる」です。
本題に入る前に,いくつかのページで「順序」を見かけました。表紙裏では,2012年刊行のNo.80の紹介として,「(略)保護者や数学者など,算数教育界外でも広く注目を集めた「順序指導」などを始め(略)」とあります。またp.53右カラムには「時にかけ算の式の順序が問題になる。」から始まる段落もあります。
少し深いところまで検討している文章を見かけました(p.26)。
加藤(2021)は,第2学年において,かけ算の数の数量関係を見出す活動を取り入れる学習指導を提案している。雪だるまを作るという場面では,雪だるま1個に対して帽子を1つ,ボタンを3つ付けるなどの条件が設定された。この条件の下で雪だるまを5個作るとき,帽子は5つ必要になる。雪だるまの数と帽子の数が同じになるのは,両者が1対1に対応しているためである。一方,ボタンの数は,雪だるまの数と1対3の対応であるため,3倍の数が必要になる。この問題では,隠れた4つ目の数である「1」を意識しながら乗法を用いて問題解決することが可能となっている。「雪だるま1個に対してボタン3つ」のように,2量を対にして1つのユニットとする(以下では,組み立てユニットと呼ぶ)ことで,2量が扱えるようになる。組み立てユニットを作り,2量を同時に繰り返して,求めたい数値を作る(ボタンは3+3+3+3+3や3×5で求められる)ことはScalar ratiosに,丸を5つ並べて書いて「雪だるま5個なら,1個にボタンは3つだから,ボタンは5×3になる」と言う児童の考えはFunctional ratesにつながると考えられる。
著者は日野圭子(宇都宮大学)です。目次の標題は「かけ算の意味指導」ですが,p.24では「比例的推論を視点として」のほうが大きめの文字になっています。
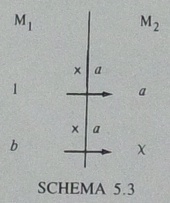
「雪だるま5個なら,1個にボタンは3つだから,ボタンは5×3になる」は,以下の図に当てはめて説明ができます。なお,この図はVergnaud (1983, p.130)によるものですが,「かけ算の意味指導」では,Vergnaud (1994)を引用しています。
当てはめは,以下の通りです。
- M1:雪だるまの個数の量空間
- M2:ボタンの個数の量空間
- a:ボタンが3つ
- b:雪だるまが5個
- x:ボタンは15個
そして「×a」にも,意味付けをすることができます。数だけ見れば3倍(「×3」)ですが,実際には,M1という量空間からM2という量空間へ変換しています。あるいは,「×a」が,M1とM2という2つの異なる量空間の仲立ちをしている,と考えることもできます*1。
引用の最初の「加藤(2021)」について,引用・参考文献をもとに検索すると,新しい算数授業研究 2021年12月号であることに気づきました*2。本棚から見つけて,加藤(2021)に当たるpp.16-19を読み直しました。雪だるまのイラストがp.17に,また「6. 1量の学習から2量の学習への広がりを経験する」(p.19)には,雪だるまとボタンの関係の言及も,あるのですが,5×3の式は見当たらず,Functional ratesへの言及も,Vergnaudの引用も,ありませんでした。
参考文献の題目でいくつか検索をしていくうちに,別の文献を見つけました。「かけ算の意味指導」の引用・参考文献には入っていません。
- 日野圭子, 上野友美, 田島達也, 秋澤克樹: 比例的推論の学習軌道に基づく授業実践の試み-小学校第3学年における実践から-, 宇都宮大学共同教育学部研究紀要, No.72, pp.613-632 (2022). http://hdl.handle.net/10241/00013138
授業実践の問題の一つは「車を作る」で,図3 (p.619)から読み取れるのは以下の内容です。
タイヤを4こと,箱2こを使っておもちゃの車を作ります。タイヤは30こあります。できるだけ多く車を作るには箱はいくつひつようで,車は何台できますか。
「箱」「車」の順に数を問うていますが,車の台数から求めるべきでしょう。30÷4=7 あまり2で,あまりの2個では1台の車を作ることはできませんので,「車は7台」です。次に箱の数です.車1台につき箱は2個必要,7台だったら…2×7=14とし*3,「箱は14こ」と表せます。
この文献では,複数の箇所で,著者らが7×2を認める(肯定的に解釈する)記述がありました。
(p.621)
また,箱の総数を求めるためにかかれた式の殆どは,7×2であり,2×7ではなかった(全体では7×2が共有された)。タイヤの数から車の台数を求めるため,まず台数が分かることになる。その7台に2つずつ箱が必要という考えから,7×2という式がかかれたのかもしれない。
(p.628)
乗法の式での予想外の反応は,2×7ではなく7×2をかく児童が多かった点である。7+7といった加法の式も見られ,児童は,7台の車に箱を1つずつ,次にまた1つずつ置いていくように,箱を割り当てていた可能性がある。
「7+7」「7台の車に箱を1つずつ,次にまた1つずつ置いていく」は,Functional ratesを,トランプ配りと結び付けて考えることができるのを示唆するように見えます*4。「全体では7×2が共有された」は気になるところで,副題の「小学校第3学年における実践」や,前後の記述と合わせると,「全体では2×7が共有された」が本旨ではないかと思われます。
*1:https://takehikom.hateblo.jp/entry/20140924/1411511070
*2:https://takexikom.hatenadiary.jp/entry/2022/12/29/062638で取り上げていました。
*3:この求め方は,Scalar ratiosに基づくものと言えます。