「さらが 5まい あります。1さらに りんごが 3こずつ のって います。りんごは ぜんぶで 何こ あるでしょう。」という出題で,「しき」の欄に「5×3=15」と書いたときにバツ印がつく(不正解とされる)理由として,以下のとおり6つを挙げていました。
- B-1: この問題では,1皿あたりのりんごの数がかけられる数であり,皿の枚数がかける数となる.
- B-2: 5×3と3×5は,かけ算の答えは同じでも,意味は異なる.
- B-3: 5×3=15の式では,皿の数とりんごの数が反対である.
- B-4: 5×3=15の式では,積は皿の枚数になってしまう.
- B-5: 単位を付けて書くと,「5個×3」と「3個×5」,「5個/枚×3枚」と「3個/枚×5枚」は,それぞれ異なる.
- B-6: 言語や文化の違いに配慮しながら式で表すことが教育上有益である.
本記事ではこのうち「B-4: 5×3=15の式では,積は皿の枚数になってしまう.」について,詳しい情報や,この理由と同様の事例を紹介していくことにします。
事例紹介の前に,「積は皿の枚数になってしまう」という理由を,累加に基づき説明します。5×3=5+5+5=15により求めたあと,全部で4回出現する「5」は何になるのかを,問題文と照合します。問題文には,「さらが 5まい」とあります。そうすると,5+5+5は,「さらが 5まい」と「さらが 5まい」と「さらが 5まい」を合わせた数となります。単位を付けて書くと,5枚×3=5枚+5枚+5枚=15枚になって,15個でないということです。
なお,「B-3: 5×3=15の式では,皿の数とりんごの数が反対である.」について,累加を取り入れ,単位を付けて書くと,5個×3=5個+5個+5個=15個となり,B-4と,数量の関係が異なっています。
それでは事例紹介です。把握している最古は,昭和26年(1951)の文書です。
三年の乗法九々の学習で,三の段がひととおりすんで,こどもたちは三の段の九々がすらすら唱えられるようになった。そこで,教師は次のようなテストを行って,こどもがかけ算の意味を理解して,九々を適用する力が伸びたかどうかを調べてみた。
問題 3人のこどもに,えんぴつを2本ずつあげようと思います。えんぴつがなん本いるでしょう。どんな九々をつかえばわかりますか。
どんな九々をつかうかという問に対して,3×2=6と答えたものが予想以上に多いことがわかった。これによってこどもは問題に出てくる数を,その数の意味を深く考えもしないで,出てくる順に書き並べ,その間に,かけ算記号を書き入れることがわかった。問題に出てくる数を頭の中にいったん収めて,演算の決定に導くように問題の場を組織だてる力が欠けているらしいことがわかった。そこで,その欠けていることについての再指導に入るわけである。
3は人数を表わしている数である。それを2倍した答の6は何といったらよいか尋ねてみる。それで,6人となって問題の要求に合わないことを説明する。このようにして3×2=6とするのが誤であることを明らかにしたとする。
「積は人数になってしまう」事例です。抜粋は最小限にしましたが,その前後まで読むと,現代の教育評価・学習評価で言うところの「形成的評価」を行っています。
次は,1998年の海外の書籍です。
章題は"Multiplicative Structures",著者はVergnaudです。メインブログの記事(トランプ配りと,うまくやっていく,かけ算と構造)より転載します。1. Connie wants to buy 4 plastic cars. They cost 5 dollars each. How much does she have to pay?
a) 5+5+5+5=20
b) 4・5=20
c) 5・4=20
d) 4+4+4+4+4=20
(1. コニーは4個のおもちゃの車を買いたい.1個は5ドルする.いくら払わないといけないか?
a) 5+5+5+5=20
b) 5×4=20
c) 4×5=20
d) 4+4+4+4+4=20)
(p.144)
The comparative facility of isomorphic over functional properties is even easier to show by considering all four procedures a, b, c, and d. Procedure b is a meaningful concatenation of procedure a. The cost of 4 cars = the cost of 1 car, plus the cost of 1 car, plus the cost of 1 car, plus the cost of 1 car. Expressed formally in terms of the isomorphic property for addition, this is f(1+1+1+1) = f(1)+f(1)+f(1)+f(1), and in terms of the isomorphic property for multiplication, f(4・1)=4・f(1). Procedure d is meaningless in terms of cars and costs. Twenty dollars cannot be 5 cars + 5 cars + 5 cars + 5 cars. Young students apparently are aware of this and never use procedure d. So there is a strong asymmetry between procedures b and c. They are not conceptually the same, although because of the commutativity of multiplication they may be mathematically equivalent.
(同型性は,4つの手続きaからdまでをまとめて検討することで,より容易に示される.手続きbは,手続きaと意味をもってつながっている.4台の値段とは,1台の値段+1台の値段+1台の値段+1台の値段である.加法における同型性を,式で表すと,f(1+1+1+1)=f(1)+f(1)+f(1)+f(1)であり,乗法における同型性によって,f(4・1)=4・f(1)となる.手続きdは,車の数と価格の観点から,無意味である.20ドルは,5台の車+5台の車+5台の車+5台の車にはなり得ない.幼い生徒たちはどうやらそのことに気づいているらしく,決して手続きdを使わない.そのため,手続きbとcの間には強い非対称性がある.それらは,乗法の交換法則によって数学的には等しいかもしれないが,概念的には同一ではない.)
(p.146)
なお,"Twenty dollars cannot be 5 cars + 5 cars + 5 cars + 5 cars."のところは,"Twenty dollars cannot be 4 cars + 4 cars + 4 cars + 4 cars + 4 cars."に置き換えることで,意図がより明瞭になります*1。
ここからは21世紀の事例です。「板書シリーズ」の先駆けとも言える本からです。
前者は2003年,後者は2011年の出版です*2。
前者の本のpp.46-47に以下の図があります。後者の本ではpp.44-45です。上下の横線が真ん中付近で切れているのは,そこがページの切れ目でして,さらに右には式が並んでおり,一つの板書例という見せ方になっています。
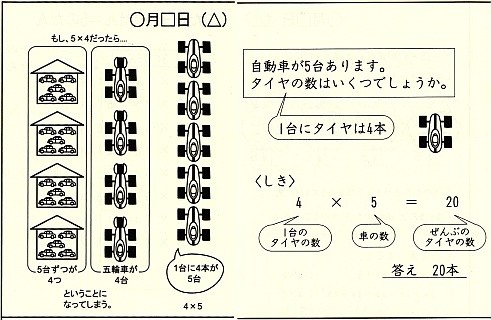
画像の見方を説明します。「自動車が5台あります。タイヤの数はいくつでしょうか」という問題から始まります。「1台にタイヤは4本」を,クラス内で共有したのち,正解となる式は「4×5=20」です。
ここでもし,「5×4」だったら,5つのタイヤがついて「五輪車が4台」となる図や,家に車が入った「5台ずつが4つ」という図が現れます(板書は容易ではなく,先生が紙に書くなどして用意しておく必要があるでしょう)。いずれも,問題に合っていません。「5台ずつが4つ」のほうが,「B-4: 5×3=15の式では,積は皿の枚数になってしまう.」と同じ解釈です。
批判的に取り上げているのは,2010年の以下の記事です*3。
該当箇所は本文で上から3番目の写真です。文字にします。
問題に出てくる数の通りに式をつくることができない7の段を適用して解く問題
(ページ番号省略)
・6×7と立式する子どもにはあめの図をかかせ,同じ数のまとまりは6なのか7なのかをしっかりとつかませる。また,6×7では、6人が7つ分になり,答えは子どもの人数となってしまうことをおさえる。
「東京書籍の指導書から引用したもの」とも書かれており,平成16年(2004年)検定の『新編 新しい算数 2下』*4に対応する教師用指導書と思われます。
また,6×8と8×6が違うこと、それを子供に教えること - 数学・算数の教材公開ページでは,上記引用について「数字はこの問題に合わせています」と断った上で書き換え,批判を行っています*5。
2019年には,「かけ算の意味理解のために、プログラミングを導入」した授業事例が報告されています(関連:リンゴの上におさらが9個~2019年の「積は皿の枚数になってしまう」事例)。
この前半(文章問題を「解く」)で使用されている文章題は,「おさらにリンゴが5こあります。おさらが9つあるとき、リンゴはぜんぶで何こありますか?」です。5×9=45の式において,「かけられる数5は1つのお皿にのっているりんごの数、かける数9はお皿の数」となります。
途中で次のように,「積は皿の枚数になってしまう」のを提示しています。
もし、かけられる数とかける数を逆に答えてしまった場合はどうなるか?
かけられる数が9、かける数が5と指定したので、式は9×5。それに対応する絵は、リンゴの上におさらが9個のっていて、そのリンゴが5個ある絵になり、プリントで設計した絵とは異なってしまう。児童にとって、この絵は驚きであった。9×5と5×9は意味が違うことが視覚的にわかる瞬間である。
この授業の事後感想で、「九九の答えは同じでも、式の意味は違う」という発言があった。場面を表す式と計算の仕方を表す式との違いに気づいた児童もいたようである。
令和4年(2022年)の全国算数授業研究会月報284号の実践報告を見ます(関連:3×2の,子どもたちの発言)。
- 全国算数授業研究会 公式HP
- 月報
- 算数授業通信284号 (令和4年8月4日)
- 実践報告①「2年「かけ算」~かけ算の意味に立ち返る授業~」(Page1879)
- 算数授業通信284号 (令和4年8月4日)
- 月報
文章題は,順に「ボールが3こずつ入った入れ物が5ほんあります。ボールはぜんぶで何こあるでしょう。」「今、教室に5人います。おり紙を1人に6まいずつくばります。おり紙はぜんぶで何まいいりますか。」で,それぞれ期待される式は「3×5」「6×5」です。
後者(おり紙の問題)では,「5×6と考えた人は12人。6×5と考えた人は14人」とあり,拮抗しています。しかし「5×6」についての理由(発言)について報告者は「意味の捉えが曖昧である」「辻褄が合わないことを言っても気づかない」と記しています*6。
ここから,「6×5」に向けるためのスイッチング・レーン*7は,「もし、5×6だったら意味が変わる」という子どもの声でした。教師がこれを拾いあげ,問い返し発問をしました。子どもたちの発言は,
「もし、5×6だったら、『教室に6人いる。一人に5枚ずつ配る』という問題文になる」「5×6だと、5は5人という人を表す。5人のまとまりごとに6つのグループをつくるという意味になる」「5×6は、式が5+5+5+5+5+5になるから問題文と合わない」と並びます。2番目の「5人のまとまりごとに6つのグループをつくる」について,同ページには「人をあらわす」として手描きの図もあります。「おり紙はぜんぶで何まいいりますか。」に,合っていません。
この実践報告は,直近の事例であるのと合わせて,「5人のまとまりごとに6つのグループをつくる」を含む発言は児童のものである点も,ここで強調しておきます。「5×6」の式の説明に「トランプ配り」を児童が発表する授業は見かけないのは,トランプ配りの乗法への適用~書籍からで抜粋した授業事例と重なります。
*1:https://www.gerard-vergnaud.org/texts/gvergnaud_1988_theoretical-frameworks_icme-6-budapest.pdf#page=9の"5 times 4 cars cannot give dollars"も関連します。ただしこの文書(招待講演の原稿)での,5ドルのおもちゃの車4つの話では,"4 cars x 5 dollars/1 car"と表せることを重要視しています。本記事冒頭のリンク先のうち,A-4と関連します。
*2:小学校算数について,東洋館出版社の板書シリーズの最新版は2020年に出ていますが,その小学校2年下[isbn:9784491040257]には,本記事で述べる図は掲載されていません。
*3:初出URLはhttps://dabun.net/news/2011_01.htm#20110105で見ることができます。【わだいのたけひこのざっき】は,メインブログの当時のブログ名でした。
*4:https://jp-textbook.github.io/%E5%B0%8F%E5%AD%A6%E6%A0%A1/2004/%E7%AE%97%E6%95%B0/214
*5:https://takexikom.hatenadiary.jp/entry/2022/12/05/055126
*6:https://www2.sed.tohoku.ac.jp/~edunet/annual_report/2011/11-06_miyata.pdfの文献の総合考察に書かれた,「Yが有していたスキーマ的知識は「かけ算の問題は,全体量=ある数×他の数という式に基づく」のような不十分な状態であったと考えられる。」と同様であるように見えます。


