かけ算の順序の昔話

算数教育について気楽に書いていきます。

6この何倍

中学校数学科 つまずき指導事典

中学校数学科 つまずき指導事典

　タイトルから想像できるように，想定する読者は中学校数学科の教師ですが，内容面ではずいぶんと，小学校算数科の話が入っています。数学の間違えやすい箇所（「はじめに」によると，「62の典型的なつまずき」）を，算数の既習事項を取り入れながら，解説しています。
　基本的には見開きが1つの項目で，右側（奇数ページ）の上部に「関連する既習事項」と題して枠で囲まれ，どんな事項をどの学年で学習するかとともに，踏み込んだ説明がなされています。「かけ算の順序」に密接に関連する文章が，p.17にありました*1。

■*2 乗法と累加の関係（小2）
　ことばの学習でもある小学校低学年では，四則演算は問題場面に対して定義されます。乗法は「～のいくつ分」で表せる問題場面で定義され，「4×3の答えは，4＋4＋4の答えと同じ」（累加）も導入されます。その定義から，「4×3は4の3つ分」，「3×4は3の4つ分」というようにその区別を学びます。「答えは同じ」という意味で4×3＝3×4とできます。それ以上計算できない「値としての式」は未習であるため，「～のいくつ分」の意味では，両辺は同じ式といえません。

　「関連する既習事項」の囲みがp.27から3ページにわたる中で，さらに箱で囲まれた，2つの設問（p.28）が，目を引きました。

①7人にえんぴつをあげます。1人に3本ずつあげるには，ぜんぶで何本いるでしょう。
②おかしが，はこに6こずつ入っています。ぜんぶの数は，6この何倍でしょう。

　問いのみで，何が正解・不正解かは明記されていませんが，①についてはその直後の「乗法は（1つ分の大きさ）×（いくつ分）＝（全体の大きさ）という状況を表す文章（関係式，等式）で導入されます」から，期待される式は，3×7＝21で，答えは21本です。
　一方，②は，（1つ分の大きさ）×（いくつ分）＝（全体の大きさ）で考えればよいとはいえ，①とは異なる難しさを含んでいます。1つ分の大きさは6（こ）ですが，いくつ分にあたる，具体的な数が，提示されていないのです。言葉の式にするなら，「6×はこの数」ですが，「何倍」と問われています。「はこの数倍」も「はこ倍」も，書いてみると違和感があります。
　具体的な数が分かれば，小学生でも（中学生による算数の復習でも）妥当な難易度となります。お菓子が6個ずつ入った箱の絵が添えられていると，その箱の数をもとに，5箱なら「5倍」と言えるわけです。


　かけ算とは別で，気になったのを2点，挙げておきます。まず，いくつかのページで，比例数直線を見かけます。これについてp.23の指導のポイントには「教科書には比例数直線はありませんが」とあり，算数偏重の中学数学解説書と感じました。同じページの図の中で「被乗数」はおかしく（被乗数にあたるのは-2だけなので），算数の用語を使うならそこは「もとにする量，比べる量」*3で，「乗数」も「割合」に読み替えたいところです。
　「1組の対辺が平行で長さが等しい四角形は，平行四辺形」に関して，pp.98-99に2箇所出現する「△ADC≡△ABC」は，「△ADC≡△CBA」と思われます。

*1:個人的には，「それ以上計算できない「値としての式」は未習であるため，」はない方がよく，「「答えは同じ」という意味で4×3＝3×4とできます。「～のいくつ分」の意味では，両辺は同じ式といえません。」とすれば明快になると，認識しています。「定義」の多用も，良いものとは思えません。

*2:原文では網掛けの角丸正方形の中に「2」

*3:ただしマイナスの量を認めるべきかという難点はあります。

みはじ (2018.09)

小学校の算数の話です．速さに関する式について，次の3つを学び，文章題などに適用していきます．

  • 速さ＝道のり÷時間
  • 道のり＝速さ×時間
  • 時間＝道のり÷速さ

（略）図を使って，この3つの式を手早く求めるための方法があります．
基本となる図は次のとおりです．

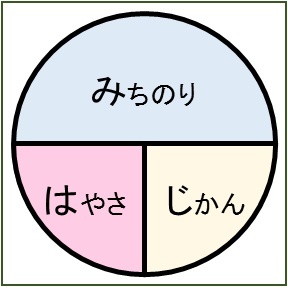
頭文字が「み」「は」「じ」ですので，くっつけて「みはじ」と呼ばれます．

みはじ・くもわ（2015.08） - わさっき

　「みはじ（はじき）」の背景となる数式を，掘り下げてみます。「速さ＝道のり÷時間」による定義（公式）を前提としたとき，この式は「道のり÷（速さ×時間）＝1」に変形できます。「みはじ」は，この左辺を図にしたものと言えます。
　みはじの図で，速さを隠すというのは，「道のり÷（速さ×時間）＝1」の両辺に速さをかけ，整理して得られる等式「速さ＝道のり÷時間」に対応します。
　速さではなく時間を隠すのは，時間を両辺にかけて整理することで，「時間＝道のり÷速さ」が得られます。
　道のりを隠す場合には，少しだけ手間を要します。両辺に（速さ×時間）をかけましょう．これで，「道のり＝速さ×時間」を導くことができます。ここまでの式変形について，中学1年で学習する「等式の性質」を使用していることもあり，小学校では扱われません。
　「速さ＝道のり÷時間」から，「道のり÷（時間×速さ）＝1」としても，代数的には，差し支えありませんが，このことに基づく「みじは（じはき）」の図は，見かけません。その理由として，一定の速さで進む（時間と道のりが比例の関係にある）とき，「速さ＝道のり÷時間」で得られる「速さ」というのは，「単位量当たりの大きさ（単位時間に進む距離）」であり，比例定数（y＝k×xのk）に対応づけられる*1のが指摘できます。
　また「速さ＝道のり÷時間」について，かわりに「速さ＝時間÷道のり」と定義することも可能ですが，そうすると，かけ算・わり算の立式（演算決定）が異なってきます。「単位時間当たりに移動する長さ」と「一定の長さを移動するのにかかる時間」とを比較すると，小学校の算数では前者が広く使われているわけです*2。
　ここまでについて「速さ」に限らず，「a＝b÷c」でaが定義でき，aとbとcが異なる種類の数量である場合に，同様に適用できます。たとえば「単価＝価格÷個数」「密度＝質量÷体積」*3について，それぞれ「価格÷（単価×個数）＝1」「質量÷（密度×体積）＝1」と表せます。Greerの分類表ではRate（比率割合）が該当します*4。別のアプローチとして，「量」に着目し，所要時間と移動距離から速さを定式化している書籍に『量と数の理論』があり，「速さ」の周辺 - わさっきで取り上げてきました。
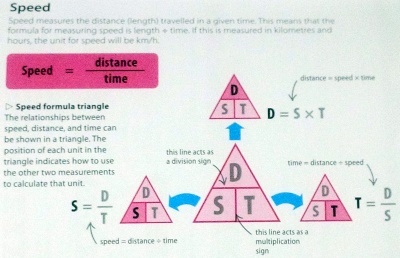
　みはじと同等の図解は，海外文献から見ることもできます。なお，それらの図が海外でも，具体的な問題を解くのに活用されているかどうかは分かっていません。ここで確認しておきたいのは，「みはじ」の3要素は異なる役割を担っており，全体として意味をなすこと，そして類似した他の用途に活用できること，ですので「みはじ」も一つの「構造」だということです。
f:id:takehikoMultiply:20180918061929j:plain*5
*6
*7
f:id:takehikoMultiply:20180918061944j:plain*8


　国内に話を戻して，算数教育における「速さ」や「みはじ（はじき）」の動向をいくつか紹介します。まず，先月発行された「算数授業研究」Vol.118*9で，田中博史氏が4マス対応表との対比として「単に公式を覚えるだけの「はじき」の図とは大きく異なる」と述べています（p.13）。同じ趣旨が『田中博史の算数授業のつくり方』*10に書かれているのですが，今年4月に東京新聞で「はじき」「くもわ」の図が掲載され，算数教育への批判がなされた記事への見解であるようにも思われます。
　「はじき」を取り入れた授業・板書の事例として，次のブログ記事があります。

　本文には「半数以上が「はじき」を知っていたことから、前時に「速さの公式」を扱った際に、「はじき」はその覚え方ということを教えました。そこで、本時では、「はじき」も認めながら、それが違う求め方でも一致するのか検討するように指導しています。」とありますが，板書の画像には，よく見かける図が出現しません。かわりに「は」「じ」「25」「x」を用いた，関係表があります。はじきを，5つの立式の根拠のうちの1つとしていますが，小さな扱いです。
　小学生が解答した，「みはじ（はじき）」では解けない，速さの問題というのも知られています。昨年書いたブログ記事より抜き出します。

　上記ブログを離れ，「速さ」や「量」を伴う出題の例に，視点を移します。算数の「速さ」の学習を通じて，数量を適切に認識し，正解が導き出せるようになってほしいと期待されている問題の一つは，おそらく以下のものであると，個人的には認識しています。
f:id:takehikoMultiply:20171128062355j:plain
　東京都算数教育研究会（都算研）が平成27年度に実施した学力実態調査で，6年生の6万人以上が解答しています。原文と解説はhttp://tosanken.main.jp/data/H28/gakuryokuzittaityousa/h27jittaityousa_kousatu_6nen.pdf#page=2より読めます。
　2つの小問のうち，(1)は「はじき」で求められます。しかし，「道のりのちがいは、何kmになりますか。」と問う(2)は，「はじき」だけでは困難と言っていいでしょう。
　B列車の速さについて，「はじき」を適用して，時速140kmを得るまではいいのですが，その次に，2つの列車の「速さのちがい」または「1時間後の道のりのちがい」を求めればよいと気づくのは，「はじき」の範囲外なわけです。
　解説では，「時速を出して、その差を5倍」のほか，「5時間後に進んだ道のりの差」を求め方として挙げています。いきなり，5時間後に進んだ道のりは出せず，1時間後の道のりを算出するのが，自然な流れですので，解説では，「どちらの方法も」と，2つの求め方を統合した上で，「単位量当たり」というキーワードを提示しています。
　正答率は(1)で91%，(2)で77%です。「調査人員 64,398人」のうち，四捨五入を考慮して76.5%としても，正答者数は49,000人を超える計算になります。これだけの子どもが，速さの応用題に対して正解を得られるというのは，学校の算数を通じて，「速さといえば，はじき」「速さ＝距離／時間」にとどまらない見方ができている，ということにならないでしょうか。

アンチはじき

　最後に，次期学習指導要領では，「速さ」は現行の第6学年から，第5学年での学習となります。次期学習指導要領の適用は2020年度からですが，移行措置により2019年度から，5年生の算数で速さを学習することになります。
　その際，「速さ」を，三用法の応用（速さ＝道のり÷時間，道のり＝速さ×時間，時間＝道のり÷速さ）として扱うのか，人口密度などと同じく「単位量当たりの大きさ」の枠内とするのかが，気になるところです。『小学校学習指導要領解説（平成29年告示）算数編』では，単位量当たりの大きさの枠内にとどまっています。
　速さを，三用法ではなく単位量当たりの大きさの中で考える（教科書や授業を通じて学習する）ことは，いまの教科書でも意図されています。それはたとえば，速さ｜算数用語集で画像になっている文章題より，知ることができます。「50m走の世界記録は5.56秒です。」に続く，「1秒間に約何m走ったことになりますか。」と「また，1m進むのに約何秒かかったことになりますか。」の設問は，それぞれ，「単位時間当たりに移動する長さ」「一定の長さを移動するのにかかる時間」を求めるのに対応します。
　先月出されたワークの編集 - 授業がんばりＭＡＴＨ - Yahoo!ブログの「どこにどう位置づけられるのか，教科書の採択が終わらなければ分からない，という苦労もあります」の箇所は，教科書の編集には携わっていないけれども地域の算数教育を主導している教師による，心情の吐露と見ることができます。


　「速さ」「みはじ（はじき）」について書いた記事を，当ブログとメインブログ（わさっき）に分けてリンクしておきます。上で引用元として挙げた記事も，再掲しています。

（タイトルを，公開当初の「かけ算の構造番外編：みはじ」から変更しました。）

*1:一定の速さで進む物体について，時間と進む道のりのペアをいくつか計測し，表にすると，時間と道のりは比例の関係にあり，道のり÷時間は決まった値をとることから，その値を速さと定義するわけです。

*2:『小学校学習指導要領解説（平成29年告示）算数編』には，「一般に速さについては速いほど大きな数値を対応させた方が都合がよいため」と書かれています。「単位時間当たりに移動する長さ」「一定の長さを移動するのにかかる時間」は，この解説と現行の解説で使用されている語句です。

*3:ただし，https://mathwords.net/mitudoのページの図では，単位量当たりの大きさに該当する密度が，右下に配置されています。

*4:量の積も一般に，「a＝b÷c」の関係においてaとbとcが異なる種類の数量となりますが，速さを含むRateにおいては，aになるものを別々に求め，それらを合併（たし算）できるとは限らないという点で異なります。時速40kmと時速100kmの電車を連結して，時速140kmで走れるわけではないのです。

*5:isbn:1593115989, p.292

*6:asin:0791417646, p.66

*7:isbn:1405322462, p.29

*8:同上

*9:isbn:9784491035642

*10:isbn:9784491023984

かけ算の構造その3：関数関係・変わり方とその周辺にあるもの

　「さらが 5まい あります。1さらに りんごが 3こずつ のって います。りんごは ぜんぶで 何こ あるでしょう。」に対して5×3＝15の式を正解とする根拠は，かけ算の順序論争について（日本語版） - わさっきのA-1からA-6でリストアップしてきたとおりですが，そこでA-4として挙げた「皿の枚数をかけられる数，1皿あたりのりんごの数をかける数と見なせばよい」について，以下の図のように表せます。
f:id:takehikoMultiply:20180913224058j:plain
　かけ算と構造 - わさっきで示した解釈を，この問題に読み替えると，次のようになります。「×3」は，数だけ見れば3倍ですが，実際には，「さらの枚数」という量空間から「りんごの個数」という量空間へ，変換しています。あるいは，「×3」が，それら2つの異なる量空間の仲立ちをしている，と考えることもできます。
　単位を付けて書くなら，「5まい×3こ/まい＝15こ」です。しかしながら，パー書きの量を積極的に採用する，数学教育協議会の人々が手がける（小学校の算数を対象とした）著書や指導例を読み直しても，パー書きの量がかける数のほうに出現する式は，ちょっと見当たりません。
　単位や団体とは別に，日本の本で上の図のような解釈を支持するものがあります。その2で紹介した，『授業に役立つ算数教科書の数学的背景』です（2013年はトランプ配り，1988年はアレイ - わさっき）。そこの記載を，今回の問題に置き換えると，「皿1枚とりんご3個の間，皿5枚とりんご15個の間に，同じ関係を認める」となります。
　ところでこの関係は，「変わり方」といった単元で，現在，4年の算数の教科書でも見ることもでき，『小学校学習指導要領解説（平成29年告示）算数編』に取り入れられています。詳細は段数×４＝周りの長さをご覧ください。https://kids.gakken.co.jp/box/sansu/04/pdf/B034407070.pdfやhttps://happylilac.net/kawari-02.pdfでも，考え方・求め方を知ることができます。
　そのほか，「時間に60をかけると分になる」や「分に60をかけると秒になる」についても，この関係をもとに説明ができます（単位の換算 - わさっき）。円周にも活用できます。具体的には，直径の長さを上の行，対応する円周の長さを下の行とする，2行（列数は任意）の表をもとに，円周＝直径×3.14という関係を確認する*1ことができます。
　この記事で述べてきた数量の関係のとらえ方は，その1で述べたのとは異なる「かけ算の構造」と言えます。『算数・数学科重要用語300の基礎知識』*2のp.187では，「関数関係に基づく乗法」と名づけています。その1で取り上げたものは，「スカラー関係に基づく乗法」です。
　それでは，4年でこの表のつくり方を学習して以降，「かけ算の順番はどちらでもいい」と，理解をしていいのでしょうか。残念ながら，「そうです」とは言えません。5年で小数のかけ算を通じて，「乗法の意味の拡張」を学んだり，6年で（かける数が）分数のかけ算を習得したりする際にも，かけられる数とかける数との違いが重視されています。

*1:ただし直径と円周はどちらも同じ単位の量であるほか，円周率は「直径が円周の何倍になるか（円周の直径に対する割合）」として定義されているため，三用法に割り当てると（第2用法では割合はかける数となるので），「円周＝直径×円周率」と表すことになる点にも，注意をしないといけません。

*2:isbn:4185007183

かけ算の構造その2：構造とは何か，そして文献整理

　「かけ算の構造」または「乗法構造」とは何かを，自分の言葉で説明してみると，次のようになります。小学校で学習する，a×b＝cという形のかけ算の式において，a，b，cにはそれぞれどのような役割があるのか，ということです．
　ここでaをかけられる数，bをかける数としなかったのは，小学校の算数の範囲でも，そうでない種類のかけ算が想定できるからです。具体的には，長方形の「縦×横」をはじめとする面積や，柱体の体積の公式である「底面積×高さ」が該当します。
　2つの因数および積の役割に加えて，その関係性が，「さらが 5まい あります。1さらに りんごが 3こずつ のって います。りんごは ぜんぶで 何こ あるでしょう。」にとどまることなく，他のどんな場面・出題にも適用できるかというのも，無視できない要素となります。
　上記に関して，「構造」の語を使用している，知る限り最も古い情報源は，1965年の座談会が活字になったものです。量，比の3用法―1965年の座談会より - わさっきから，取り出しますと，中島健三が「比の用法は複雑だというご意見ですが，乗法・除法の適用の場を構造として捉えると，あのような形にまとめられるということです。」と発言している箇所です。かけ算の式は出ておらず，発言者は，構造とは何かを明示していませんが，「比の用法」は，「割合の3用法」*1といった呼び名に変わり，現在も活用されています*2。
　「乗法・除法の適用の場を構造として捉える」に関しては，Greerによる分類表が知られています。Greerによる，乗法・除法が用いられる場合 - わさっきで和訳を試み，かけ算・わり算でモデル化される場面では画像にしました。特徴としては，「3用法」に対応づけられる，かけられる数とかける数の区別のあるかけ算と，そういった区別のないかけ算が，念頭に置かれていることです。「さらが 5まい」から始まる，りんごの文章題は，Equal groups（同等のグループ）に分類されます。「縦×横」はRectangular area（長方形の面積）なのに対し，「底面積×高さ」は，2つの因数と積がいずれも異なる種類の量である点に注意すると，Product of measures（量の積）の事例と考えるべきでしょう。なお，https://books.google.co.jp/books?id=oVlHAAAAQBAJ&pg=PA934#v=onepage&q&f=falseより読めるBrian Greerのプロフィールの中に，second phase（1983-1996年）の活動の最初の項目としてmultiplicative structureが挙げられています。
　その1で記したVergnaudの「Multiplicative Structures」について，かけ算と構造 - わさっきにて「かけ算の順序」に焦点を当て，取り上げていました。そこで参考文献として挙げた[柏木2011]は，現在はデッドリンクですが，http://repository.lib.tottori-u.ac.jp/3498より論文を無料でダウンロードでき，乗法構造や概念領域(conceptual field)について，詳しく解説されています。
　他に「構造」と明記された，関連しそうな記載を，簡潔に並べておきます。

  • 『授業に役立つ算数教科書の数学的背景』*3 p.10（執筆者は小原豊）：算数・数学の問題解決を乗法構造という立場から特徴づけて捉えるベルニョの見解によれば...
  • 「比の学習における小学生による説明と式の利用」*4 p.1：乗法構造は重要な学習内容であるにも関わらず、学習者の理解が十分ではないという状況は近年においてもあまり改善されてきていないように見受けられる...
  • 「かけ算の導入」*5 p.50：これは，一つ分が明示的でない場合に，自分で一つ分を設定し，場面を（一つ分の大きさ）×（幾つ分）として構造化し，表現することを経験するもので...

　また，現行と次期の『小学校学習指導要領解説算数編』を読み比べると，「かけ算の構造」と関連する「構造」の使われ方があるのに気づきました。それぞれの解説は，以下よりPDFファイルが入手できます。

　PDFのビューアで検索した限り，現行の解説での「構造」の出現は，「「算数的活動を通して」...が目標の全体にかかっているという基本的な構造」と「十進構造」の2箇所のみです。次期解説では「算数的活動」がなくなった（数学的活動に取ってかわった）一方で，改定の経緯の最初の段落に「社会構造や雇用関係は大きく，また急速に変化しており」とあります。また学年の目標および内容の中に「十進構造」を見ることができます。これらについては同等と言えます。
　新たな「構造」の使われ方は，次の2つです。まず第2学年，加法と減法の相互関係で，「...数量の関係がつかめないときや，解決の仕方が分からないときには，問題場面に沿って図に表すことで問題の構造がつかみやすくなったり，正しい計算を見いだしたりすることなどを確認し，図という数学的な表現のよさに気付かせることが大切である。」とあります。もう一つは第3学年の目標で「身の回りの数や数量の関係への関心を高め，数についての感覚を一層豊かにするとともに数の大きさや構造に着目して表し方を考え，日常生活に生かせるようにする。」という文です。
　いずれも直接的に，「かけ算の構造」を指すものではありませんが，Vergnaudは「Multiplicative Structure」に先立ち，additive structure（たし算の構造）に関する解説をフランス語で作成していますし，第3学年では例えば「20×4」を，累加とは別の方法で計算できる*6ことを学んでから，23×45などの計算に活用することになります。


　日本科学未来館で開催の，「デザインあ展 in TOKYO」で，Structureと書かれた看板が，吊り下げられていました。
f:id:takehikoMultiply:20180914194944j:plain
　とはいえその展示の英語の解説には，structureの語を見かけず，代わりに使用されていたのは「parts」でした。
　部分と全体の関係，そして「構造（しくみ）」を意識しながら，モノづくりではなくヒトづくりとなる教育について，今後も動向を見守ることにします。

*1:http://www.shinko-keirin.co.jp/keirinkan/sansu/WebHelp/05/page5_23.htmlで見ることのできる式は「p＝A÷B」「A＝B×p」「B＝A÷p」で，このときAとBは同じ種類の数量となるのに対し，割合のpは無次元量として扱われます。

*2:https://ci.nii.ac.jp/naid/120006466709の「機関リポジトリ」ようり入手可能な論文では，小学校学習指導要領解説算数編（前半）を引用の上，「この三つの関係性は，割合の三用法として知られている」と記しています。ただし引用した文献（PDF）で「用法」を検索しても見当たりません。

*3:isbn:9784491029641

*4:http://hdl.handle.net/10513/2146

*5:http://ci.nii.ac.jp/naid/110007994852

*6:累加だと，20×4＝20＋20＋20＋20＝80です。他の方法というのは，20を，10が2つとみていったん10を除外し，2×4を計算したあと，10倍します。あえて式で表すと，20×4＝10×2×4＝10×8＝80ですが，このような式変形を小学校で学習するわけではありません。

かけ算の構造その1：かけられる数とかける数に着目すると

例えば「さらが 5まい あります。1さらに りんごが 3こずつ のって います。りんごは ぜんぶで 何こ あるでしょう。」に対して「5×3＝15」としたら，「5個ずつ3皿」や「5枚×3で15枚になる」といった読み取り方を，挙げることができるのです。

順序の強制か，意味の理解か

　図にしてみました。

　ただし表にすることは，主眼ではありません．二重数直線や，「1:3＝5:15」といった比（比例式）に置き換えても，同じように表現することができます。それから，問題文に「1」があるから，表に1を書いた，というわけでもありません。「3人に5個ずつ」や「6人のグループがちょうど5つできました」といった，「1」が明示されていない場面でも，「1人に5個」「1つのグループは6人」と書くことができ，1が内在しているのです。
　この図を通して見ることのできる「かけ算の構造」は，次のとおりです。かけられる数と，かけ算の答えは，同じ種類の数量（ここではりんごの個数）です。かける数について，（正解となる式の）「5」は，「さらが 5まい」の意味を離れ，「皿の数が1枚から5枚になること」を意味し，「5つ分（5倍，×5）」になる，というわけです。
　単位を添えて書くと，明確になります。正解の「3×5＝15と書いたら…」については，「3こ×5＝15こ」です。「5×3＝15と書いたら…（その1）」は「5こ×3＝15こ」，「5×3＝15と書いたら…（その2）」は「5まい×3＝15まい」と表すことができまして，いずれも，左上の画像（問題として書かれた場面）に合っていないというわけです。
　「さらが 5まい」が，「5つ分（5倍，×5）」になるのは，この文脈では，皿の枚数とりんごの個数が比例関係にあるためです。皿の数が2倍，3倍，…になれば，それに応じて，りんごの数も2倍，3倍，…になる，という関係です。比例関係や倍概念を学習していない段階であっても，図にすることで，「5枚の皿に3個ずつ」と「3枚の皿に5個ずつ」が描き分けられますし，「かける数が1ふえると，かけ算の答えはかけられる数だけふえます」というのは，2年のかけ算の単元を通じて学習します。
　ここまでについて，本記事公開後に読み書きしたものを取り入れながら，関連情報を挙げることにします。「さらが 5まい あります」から始まる画像と不正解への批判は，2010年11月にまとめられたかけ算の5×3と3×5って違うの？ - Togetterより見ることができます。「5×3＝15と書いたら…（その1）」と「5×3＝15と書いたら…（その2）」は，かけ算の順序論争について（日本語版） - わさっきhbのB-3とB-4にそれぞれ対応します。また（その2）については，かけ算の意味理解のために，プログラミングを導入したという授業にも出現します（リンゴの上におさらが9個～2019年の「積は皿の枚数になってしまう」事例）。かける数が，与えられた場面では「5まい」のように単位を伴う（純粋な数ではなく，具体的な量を表す）のに，かけ算にすると「5倍」に読み替えられることについては，Vergnaudが1983年と1988年，異なる編著の書籍に「Multiplicative Structures」という章題（日本語に訳せば「かけ算の構造」です）で書いた，構造の一つ*1のほか，中島健三『算数・数学教育と数学的な考え方』に出現する「かけ算の本質（構造）」*2が密接に関係し，（日本の）算数では5年の，かける数が小数になる際の「乗法の意味の拡張」を学習する段階で，より意識することとなります。表にすることで違いを把握するという，2年生を対象とした授業事例については，『数学教育学の礎と創造―藤井斉亮先生ご退職記念論文集―』という本に載っており，8×3を，表から見つけるで紹介しています。

*1:http://d.hatena.ne.jp/takehikom/20140924/1411511070

*2:http://d.hatena.ne.jp/takehikom/20150720/1437344285

2005年の検定外の算数教科書のかけ算の順序

　2005年の，小学校の先生向けの本にも，「2つの数を出現の反対の順にしてかける文章題（出現順だと正解ではない）」「アレイ（2つの数を入れ換えた式も正解）」などが，特に断りなく取り入れられていました。書かれていなくても当たり前の事項だったと推定できます。


検定外・学力をつける算数教科書〈第1巻〉第1学年編

検定外・学力をつける算数教科書〈第1巻〉第1学年編

検定外・学力をつける算数教科書〈第2巻〉第2学年編

検定外・学力をつける算数教科書〈第2巻〉第2学年編

　テープ図を批判するより前にで紹介した「プリントによる全体・部分集合の学習」が書かれているのは，第1学年編のほうです。
　どちらの本にも，目次の前に，監修者・横地清氏による編集の趣旨が2部構成で書かれています。当時の検定教科書や学習指導要領の欠陥を指摘する中で，p.4に太字で書かれた「今日の子どもは早くから地球時代，宇宙時代，さらにはIT時代の世界に生きていると言ってよい。」が，いろいろな意味で時代を感じさせます。この本から離れますが，「宇宙時代」で連想するのは，オーリという商品であり，テレコンワールドというテレビ番組です。1990年代中ごろ，深夜によく目にしました。*1
　さて，手元にあるのは第1学年編と第2学年編のみですが，p.6と，ジャケットの見返し部分の記載を合わせると，作成グループと学年との対応付けは以下のようになります。そして横地氏は，すべての監修に携わったという位置づけです。

  • 「大阪研究グループ」は第4学年編・第5学年編
  • 「山形研究グループ」は第1学年編・第3学年編
  • 「山梨研究グループ」は第2学年編・第6学年編

　かけ算より前に，第1学年編のp.143から始まる「集合と論理」をざっと見ておきます。はじめに教師向けの解説文に3ページを割いています。そしてp.143の下部には，「「新算数4年1」大日本図書，1961，38-39より」として，教科書の見開きが載っています。その見開きから読み取れる，集合の記載例は「｛②　③　⑤　⑥　⑦｝……(ア)」「｛①　②　③　④　⑤　⑥　⑦｝…(イ)」「｛①　④｝……(ウ)」です。それらの集合表記より上（同じページ）では，箱囲みで，①から⑦までを左から右に並べ，それぞれに縦書きで人物名を書いています。要素をカンマで区切っていませんが，集合の外延的記法と同等と見なせる書き方です。
　それに対し，p.146から始まる子ども向けの絵および文章では，「かこんだ ぜんぶのしゅうごうのなかで，左のえのように，おとこのこは 4にん います。おとこのこのあつまりを，「おとこのこのしゅうごう」と呼びます。」となっています。それぞれの男の子の区別は重要視されていませんし，あとの出題（例えばp.148の3問はいずれも「～のしゅうごうはなんにんですか。」です）からも，多重集合を扱っているのが確認できます。
　ではかけ算に移ります。第2学年編のp.72からです。
　かけ算の言葉の式として，p.73では「同じ数」×「回数」と書いてあります。また子ども向けにはp.81の最下段に「おなじ数×いくつぶん＝ぜんぶの数」となっており，かけられる数と積は同じ種類の数になるのが含まれています。Greerの分類表のうち，Equal groupsは「同じ数ずつ」，Equal measuresは「同じ量ずつ」と訳すのがよさそうに思えてきました*2。
　「かけられる数」「かける数」の用語はp.77で，初出は太字になっています。そのすぐ下には，6×4＝4×6の式と，「かけざんでは，かけられる数とかける数を入れ換えても，こたえは同じです」すなわち交換法則のことが，書かれています。さらに「2×8＝14＋2＝16」などの式があり，これは小学校算数の学習指導要領に書かれている「乗数が1ずつ増えるときの積の増え方」に対応するものです。かけ算を段ごとに学習するより前のところで，これらが一括して取り扱われているのは，現在の教科書に見かけない独自性と言っていいかもしれません。
　かけ算の順序を問う問題*3も，ありました。少しページを進めて，p.88の「かんがえよう」の大問2です。「子どもが7人います。1人におりがみを5まいずつくばると，ぜんぶでなんまいいるでしょうか。」という問題文の下に，「（しき）」と「こたえ」の欄があります。p.105の解答を見ると「5×7＝35　35まい」となっていて，式にする際には5が先，7があとです。
　ほかにp.113の「ゆりこさんは，8人の人からお年玉をもらいました。どのふくろにも，3000円ずつ入っていました。ぜんぶで，お年玉はいくらだったでしょうか。」と，p.119の「③ チョコレートを2はこかいました。1はこの中にチョコがたて4こで，よこに6れつならんでいます。(1) 2はこではチョコはぜんぶんでなんこでしょうか。」（式は「4×6×2＝24×2＝48　48こ」）も該当します。
　タイルの2次元配置を見ることもでき，p.100のまとめの大問1②は，3行6列の並びで，解答には3×6＝18と6×3＝18を挙げています。なお大問1①は，4行4列の並びで，式は4×4＝16のみです。
　「あきらくんの家では，ほしがきをたくさんつくっています。1つのならに4こずつつるしてあります。そのなわがぜんぶで200本あります。かきは，ぜんぶでなんこあるでしょう。」(p.116)の式には「4こ×200本＝」で，等号の右は空欄です。すぐ下に，バラ数による計算のあと「こたえ 800こ」としています。「かける数とかけられる数をいれかえて，計算してみました。」という文と，200×4＝800のバラ数表記の式が，続きます。交換法則は，計算の性質である（ほしがきの文章題において「200×4」または「200本×4こ」という式を立てることは，想定されていない）のを示唆しています。
　バラ数は別として，以下のことは，現在の算数教科書との共通点となっています。

  • かけられる数とかける数は明確に区別されている。
  • 「式に表す」「式を読む」活動において，かけられる数と積は同じ種類の数量である。
  • アレイ（2次元配置）では，2つの数を入れ換えた式も認められる。
  • 立式した上で，計算（たしかめ）において交換法則の適用がなされている。
  • 2つの数を出現の反対の順にしてかける（式に表す）文章題が入っている。

　これに関してp.6の「各研究グループには実践と研究の豊かな，肝入りの小学校の現場の校長，指導主事，先生方がたくさんそろっている。」が興味深いところです。最初に読んだときは，内容の保証をするいわば宣伝文句ととらえたのですが，書籍の中で明示されていない上記の5項目は，そのころの先生方にとっては書かれていなくても当たり前の事項だったと，考えられるのです。

*1:そのほか「IT」に関して，総務省が「IT政策大綱」を「ICT政策大綱」に改めたのは2004年ですが，「検定外・学力をつける算数教科書」のシリーズを執筆している段階で，この変革に対応していないと言うのは酷というものでしょう。なお，情報通信関連の最近のトピックといえば，IoT（モノのインターネット）です。https://hnavi.co.jp/knowledge/blog/ict/に，IT・ICT・IoTの違いがわかりやすく記されています。

*2:本記事で取り上げている第2学年編において，子ども向けの記載に「ずつ」がたびたび出現しますが，必須ではなく，「1はこ8こいりのおかし4はこぶんでなんこ。」「1本9cmのリボン7本ぶんでなんcm。」（いずれもp.86），「6人のグループがちょうど5つできました。」（p.101）のように，「ずつ」なしの出題も載っています。いずれも式で表すと，かけられる数の単位は，求めたい量の単位と一致します。

*3:http://d.hatena.ne.jp/takehikom/20131229/1388265996

被乗数・乗数と因数の間に，係数を

　チョコバナナクレープ1個の値段をa円としたとき，200個を売ったのなら，売り上げを表す式はa×200となります。小学算数6年の「文字を用いた式」と関連します。
　それに対し，中学1年では例えば200a円と書くことになります．他の表記，そして「チョコバナナクレープ」については，「1個a円の品物の3個の代金」を表す文字式は，（a×3）円か，a×3（円）かをご覧ください。
　「a×200」や，そのもととなる言葉の式の「単価×個数」において，乗算記号「×」の左に書かれるのは，かけられる数（被乗数，multiplicand）です。右に書かれる，かける数（乗数，multiplier）がそこに作用し，売上額の算出に使われるというわけです。
　それに対し「200a」と書いたら，それは「200×a」と解釈できるのは事実ですが，その際，200を被乗数，aを乗数と，認識しているわけではありません。
　代わりに適切な言葉があります。因数（factor）です。200とaは，200aの因数となります。文字式だけでなく，整数を積の形で表記するときにも，この語は使用され，式の計算|因数とは何か|中学数学|定期テスト対策サイトの例によると，36＝1×36と表したのであれば，1と36が（36の）因数であり，36＝2×3×6だと，2と3と6が（36の）因数となります。因数は，中学3年で学習する語*1です。
　被乗数と乗数の区別や，「作用」といった考え方は，日本に限ったことではなく，例えばGreer (1992)にも記載されています*2。その文献の分類表*3には，被乗数と乗数を区別する（asymmetricな）タイプを7種類，区別しないタイプを3種類，記載しています。「被乗数×乗数」「因数×因数」と，書き分けることもできます。
　「200とaは，200aの因数」というのは，いわば200とaとを対等に見る立場ですが，aという文字（あるいは変数）に着目するとなると，左に書かれる200は，因数と異なる名称で呼ばれます。係数（coefficient）です。中学1年で学習する語です。
　200aにおいて，aの係数は200です。x^2+2x-35という，xの2次式を考えるなら，x^2の係数は（x^2＝1×x^2に注意して）1です。xの係数は，2です。最後の「－35」は，定数項ですが，x^2+2x-35＝a_2x^2+a_1x-a_0に対応づけると，このa_0＝－35も，係数と見なすことができます．そのような扱いは，wikipedia:係数で読むことができるほか，現行および次期の『中学校学習指導要領解説数学編』にも，二次方程式の解の公式を解説する中で，「ax^2+bx+c=0の解が三つの項の係数a，b，cで定まる」と記されています。
　「200aと表したとき，aの係数は200である」という文は，「aを200倍すると，200aである」と理解することもできます。累加で表すこともできて，a＋a＋…＋a＝a×200＝200aです*4。ここで「a×200」は，累加に基づくかけ算の式表現であるとともに，単価a円の商品を200個を売ったときの売り上げを表す式にもなっています。
　別の文字式を考えてみます。チョコバナナクレープ1個の値段を150円としたとき，b個を売ったのなら，売り上げを表す式は，小学6年では150×bが，中学1年では150b円が，それぞれ期待されます。
　150bにおいて，bの係数は150です。そしてb＋b＋…＋b＝b×150＝150bと表せますし，「bを150倍すると，150bである」とも言えます。このように，bを被乗数，150を乗数に，対応づけることができます*5。「単価×個数」という言葉の式による割り当てだと，150が被乗数，bが乗数と解釈されますが，bを被乗数としても乗数としてもよい，あるいはb×150にも150×bにもなるというのは，文字式を対象とした乗法の交換法則を，我々は当然のものとして使用しているからと言えます。
　かけ算を累加でとらえるのは，係数が（正の）整数の場合に限られます。そうでない場合，例えば\frac{1}{3}xや－7yにおいて，\frac{1}{3}と－7は，それぞれxとyの係数となります。そしてxやyという文字に着目すると，「xを\frac{1}{3}倍すれば\frac{1}{3}x」「yを－7倍すると－7y」ですので，係数が乗数の役割を果たす*6ことが，正の整数でない状況からも，確認できます。

*1:平成20年告示の中学校学習指導要領の数学はhttps://erid.nier.go.jp/files/COFS/h19j/chap2-3.htm，平成29年告示についてはhttps://erid.nier.go.jp/files/COFS/h29j/chap2-3.htm

*2:https://takehikom.hateblo.jp/entry/20151121/1448031600

*3:https://takexikom.hatenadiary.jp/entry/2019/09/10/211914, https://books.google.co.jp/books?id=N_wnDwAAQBAJ&lpg=PR1&hl=ja&pg=PA280#v=onepage&q&f=false

*4:200＋200＋…＋200＝200×a＝200aと解釈することも，aが正の整数であれば，差し支えありません。

*5:数学の文字式に限ったものではなく，日常の数量表現に目を向けると，「15人」「3メートル」についても同様に，「15人は1人の15倍」「3メートルは1メートルの3倍」と考えることができます。「15人は15の人数倍」「3メートルは3のメートル倍」とは言いません。

*6:1個の実数値（スカラー量）という制約を外すと，wikipedia:アフィン変換に見られる行列とベクトルの積の形や、https://triple-underscore.github.io/SVG11/coords.htmlの「3x3 の 変換行列」を用いた座標系変換と関連付けることができます。その場合，スカラー量の議論での文字はベクトルに，係数は変換行列に，それぞれ対応します。