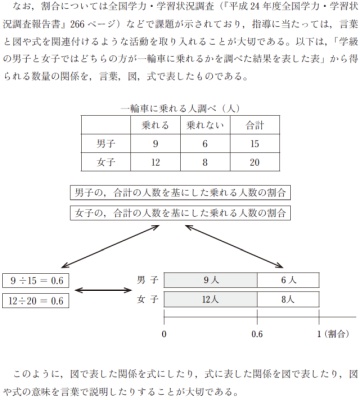
第5学年
四角形の四つの角の和を基に説明する方法の代表的なものとして,次の二つの方法がある。①は四角形を1本の対角線で二つの三角形に分けて考える方法で,三角形の三つの角の大きさの和が180度であることを基にして,180度の2倍から360度を導き出す方法である。②は四角形の内部に点Eをとり,点Eと各頂点とを結んだ直線で四つの三角形に分けて考える方法で,三角形の三つの角の大きさの和が180度であることを基にして,180度の4倍から点Eの周りの角の大きさである360度を引いて360度を導き出す方法である。
(p.254)
(p.270)
台形の面積の求め方として,例えば次の二つの場合を児童が考えたとする。
「台形を二つ合わせて平行四辺形にしました。底辺が(2+8)で高さが4なので平行四辺形の面積が求められます。その面積の半分なので÷2をしました。(2+8)×4÷2=20です。」
「台形を横に切って一部を移動して平行四辺形にしました。底辺が(2+8)で高さが4÷2なので,(2+8)×(4÷2)=20です。」
などのように考えたことを伝え合い,お互いの考えを共有していく。
(p.282)
台形を二つ合わせて平行四辺形にする考えでは,次のように考えるだろう。
このことから((上底)+(下底))×(高さ)÷2という台形の公式を導くことができ
る。
また,台形を横に切って一部を移動して平行四辺形にする考えでは,次のように考えるだろう。
このことからも((上底)+(下底))×(高さ)÷2という台形の公式を導くことができる。
このように幾つかの求め方を公式にしていき,どの求め方からも((上底)+(下底))×(高さ)÷2が導けることを確認して公式としてまとめる。
これらの経験を通して,図と式を関連付けて考える力や,式に表現したことを公式という簡潔・明瞭・的確な表現に高めていく力の育成を目指す。
(p.283)
他の学年
具体物を等分することについては,全体を同じ数ずつ幾つかに分けたり,全体を幾つかに同じ数ずつ分けたりすることができるようにする。例えば,8本の鉛筆を,2本ずつや4本ずつなど,同じ数ずつ分けると何人に分けられるかを操作や図で説明したり,分けられた結果を式に表したりする。このようなことを通して,8という一つの数を多面的にみることができるようにし,数についての感覚を豊かにする。
(p.81)
加法の場合には様々な計算の仕方が考えられる。その主なものとしては,加数を分解する場合と被加数を分解する場合がある。例えば,8+7の場合,加数の7を分けて(8+2)+5としたり,被加数の8を分けて5+(3+7)としたりして,数を分解して加えて10をつくり,10と5で15と計算する。
(p.87)
例えば,「12 個のおはじきを工夫して並べる」という活動を行うと,いろいろな並べ方ができる。下の図のように並べると,2×6,6×2,3×4,4×3などのような式で表すことができる。このように,一つの数をほかの数の積としてみることができるようにし,数についての理解を深めるとともに,数についての感覚を豊かにする。
(p.106)
また,「内容の取扱い」の(3)では,「乗数又は被乗数が0の場合の計算についても取り扱うものとする」と示している。例えば,的当てで得点を競うゲームなどで,0点のところに3回入れば,0×3と表すことができる。3点のところに一度も入らなければ,3×0と表すことができる。0×3の答えは,実際の場面の意味から考えたり,乗法の意味に戻って0+0+0=0と求めたりする。また3×0の答えは,具体的な場面から0と考えたり,乗法のきまりを使って3×3=9,3×2=6,3×1=3と並べると積が3ずつ減っていることから,3×0=0と求めることができることに気付くようにする。
(p.143)
また,除法は,乗法の逆算ともみられる。そこで,乗法と関連させて,被乗数,乗数のいずれを求める場合に当たっているかを明確にすることも大切である。等分除は,□×3=12の□を求める場合であり,包含除は3×□=12の□を求める場合である。
(p.148)
例えば,「500円玉をもって買い物に行き,150円のジュースと260円のパンを買いました。おつりはいくらですか」という問題がある。次のように式に表すことができる。
500−(150+260)=90 ジュースとパンをまとめて買った場合
500−150=350 350−260=90 ジュースとパンを別々に買った場合
もしも,500円玉1枚ではなく,100円玉5枚をもって行ったとすると,(200−150)+(300−260)=90と表すこともできる。
(p.198)
例えば,分数の意味と表現に着目して,乗数を単位分数の幾つ分とみると,
という分数の乗法を次のように計算することができる。
また,乗数のを2÷3の結果とみると,次のように求めることができる。
計算に関して成り立つ性質に着目することとは,乗法に関して成り立つ性質や除法に関して成り立つ性質,交換法則,結合法則などの四則に関して成り立つ性質に着目することである。
例えば,除法に関して成り立つ性質を用いると,という分数の除法を次のように計算することができる。
と求めることもできる。
(pp.288-289)